მატერიის აირისებრი აგრეგატული მდგომარეობის თერმოდინამიკა არის ფიზიკის მნიშვნელოვანი ფილიალი, რომელიც სწავლობს თერმოდინამიკურ წონასწორობას და კვაზი-სტატიკურ გადასვლებს სისტემებში. მთავარი მოდელი, რომელსაც ეფუძნება სისტემების ქცევის პროგნოზები, არის იდეალური გაზის მოდელი. მისი გამოყენებით მიიღეს მენდელეევ-კლაპეირონის განტოლება. განიხილეთ ეს სტატიაში.
იდეალური გაზი
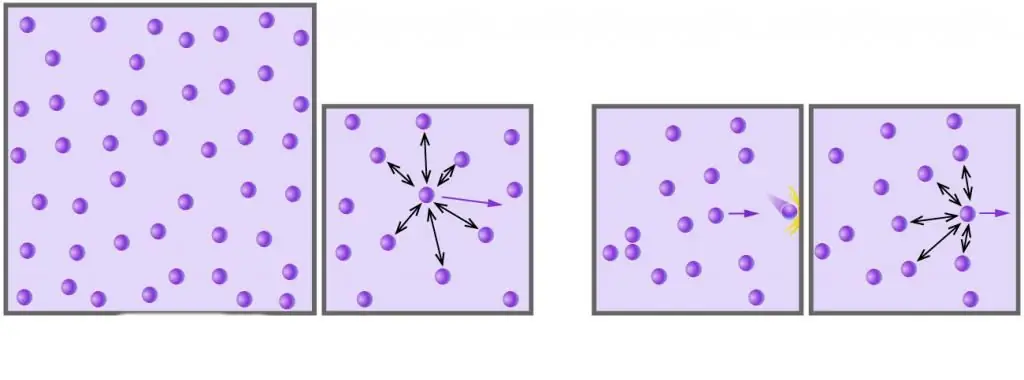
როგორც მოგეხსენებათ, ყველა რეალური აირი შედგება მოლეკულებისგან ან ატომებისგან, რომელთა შორის მანძილი ძალიან დიდია მათ ზომასთან შედარებით დაბალი წნევის დროს. გარდა ამისა, მაღალ ტემპერატურაზე, აბსოლუტური მასშტაბით, მოლეკულების კინეტიკური ენერგია აღემატება მათ პოტენციურ ენერგიას, რომელიც დაკავშირებულია სუსტ დიპოლ-დიპოლურ ურთიერთქმედებებთან (თუ ამ ურთიერთქმედების გარდა, არსებობს სხვა სახის ქიმიური ბმები, მაგალითად, იონური ან წყალბადი, შემდეგ ისინი მნიშვნელოვან წვლილს შეიტანენ შიდა სისტემის ენერგიის პოტენციურ კომპონენტში).
გამობევრი რეალური გაზისთვის ნორმალურთან მიახლოებულ პირობებში შეიძლება უგულებელყო მათი შიდა ურთიერთქმედება და ნაწილაკების ზომები. ეს ორი ძირითადი მიახლოება წარმოადგენს იდეალურ გაზის მოდელს.
მენდელეევის განტოლება ფიზიკაში

უფრო სწორი და სამართლიანია ამ განტოლებას კლაპეირონ-მენდელეევის კანონი ვუწოდოთ. ფაქტია, რომ ის პირველად ჩაწერა ფრანგმა ინჟინერმა ემილ კლაპეირონმა 1834 წელს. მან ეს გააკეთა ბოილ-მარიოტის, გეი-ლუსაკის და ჩარლზის გაზის კანონების ანალიზით, რომლებიც აღმოჩენილი იქნა მე-19 საუკუნის დასაწყისისთვის.
რუსი ქიმიკოსის დიმიტრი მენდელეევის დამსახურება მდგომარეობს იმაში, რომ მან განტოლებას თანამედროვე და ადვილად გამოსაყენებელი მათემატიკური ფორმა მისცა. კერძოდ, მენდელეევმა განტოლებაში შემოიტანა მუდმივი ყველა გაზისთვის R=8, 314 J/(molK). თავად კლაპეირონმა გამოიყენა მთელი რიგი ემპირიული მუდმივები, რომლებიც ართულებს გამოთვლით პროცესს.
მენდელეევ-კლაპეირონის განტოლება იწერება შემდეგნაირად:
PV=nRT.
ეს ტოლობა ნიშნავს, რომ P წნევის და V მოცულობის ნამრავლი გამოხატვის მარცხენა მხარეს ყოველთვის პროპორციულია აბსოლუტური ტემპერატურის T ნამრავლისა და n ნივთიერების რაოდენობაზე მარცხენა მხარეს.
შესწავლილი გამოთქმა საშუალებას გაძლევთ მიიღოთ ნებისმიერი გაზის კანონი, თუ დააფიქსირებთ მის ოთხი პარამეტრიდან ორს. იზოპროცესების შემთხვევაში შესწავლილია დახურული სისტემები, რომლებშიც არ ხდება მატერიის გაცვლა გარემოსთან (n=const). ეს პროცესები ხასიათდება ერთი ფიქსირებული თერმოდინამიკური პარამეტრით (T, P ან V).

პრობლემის მაგალითი
ახლა მოვაგვაროთ პრობლემა მენდელეევ-კლაპეირონის განტოლებაზე. ცნობილია, რომ ჟანგბადი, რომლის წონაა 500 გრამი, არის 100 ლიტრი მოცულობის ცილინდრში 2 ატმოსფეროს წნევით. რა არის ტემპერატურა ბუშტში, იმის გათვალისწინებით, რომ სისტემა თერმოდინამიკურ წონასწორობაშია.
შეგახსენებთ, რომ განმარტების მიხედვით, ნივთიერების რაოდენობა გამოითვლება ფორმულით:
n=მ/მ.
სადაც m არის სისტემის ყველა ნაწილაკების მასა, M არის მათი საშუალო მოლური მასა. ეს ტოლობა საშუალებას გვაძლევს გადავწეროთ მენდელეევის განტოლება შემდეგი ფორმით:
PV=mRT/M.
სად მივიღებთ ამ ამოცანის სამუშაო ფორმულას:
T=PVM/(mR).
რჩება ყველა სიდიდის გადაქცევა SI ერთეულებად და მათი ჩანაცვლება ამ გამოსახულებაში:
T=21013250, 10, 032/(0, 58, 314)=156 კ.
გამოთვლილი ტემპერატურაა -117 oC. მიუხედავად იმისა, რომ ჟანგბადი ამ ტემპერატურაზე კვლავ აირისებრია (ის კონდენსირდება -182,96 oC-ზე), ასეთ პირობებში იდეალური გაზის მოდელის გამოყენება შესაძლებელია მხოლოდ გამოთვლილი მნიშვნელობის ხარისხობრივი შეფასების მისაღებად.






