ყველა სკოლის მოსწავლემ იცის, რომ სინათლე ერთგვაროვან გამჭვირვალე გარემოში მოძრაობს სწორ გზაზე. ეს ფაქტი საშუალებას გვაძლევს განვიხილოთ მრავალი ოპტიკური ფენომენი სინათლის სხივის კონცეფციის ფარგლებში. ეს სტატია საუბრობს სხივის დაცემის კუთხეზე და რატომ არის მნიშვნელოვანი ამ კუთხის ცოდნა.
სინათლის სხივი არის მიკრომეტრიანი ელექტრომაგნიტური ტალღა
ფიზიკაში არის სხვადასხვა ხასიათის ტალღები: ბგერა, ზღვა, ელექტრომაგნიტური და სხვა. თუმცა, ტერმინი „სხივი“ეხება მხოლოდ ელექტრომაგნიტურ ტალღებს, რომელთა ნაწილიც ხილული სპექტრია. თავად სიტყვა "სხივი" შეიძლება წარმოდგენილი იყოს როგორც სწორი ხაზი, რომელიც აკავშირებს სივრცეში ორ წერტილს.
სინათლე (როგორც ტალღა) შეიძლება ჩაითვალოს როგორც სწორი ხაზი, რადგან თითოეული ტალღა გულისხმობს ვიბრაციების არსებობას. ამ კითხვაზე პასუხი მდგომარეობს ტალღის სიგრძის მნიშვნელობაში. ასე რომ, საზღვაო და ხმის, სიგრძე რამდენიმე სანტიმეტრიდან ათეულ მეტრამდე მერყეობს. რა თქმა უნდა, ასეთ რხევებს ძნელად შეიძლება ეწოდოს სხივი. სინათლის ტალღის სიგრძე ერთ მიკრომეტრზე ნაკლებია. ადამიანის თვალს არ ძალუძს ასეთი ვიბრაციების გარჩევა, ამიტომ გვეჩვენება, რომრომ ჩვენ ვხედავთ პირდაპირ სხივს.
სისრულისთვის, უნდა აღინიშნოს, რომ სინათლის სხივი ჩანს მხოლოდ მაშინ, როდესაც ის იწყებს გაფანტვას მცირე ნაწილაკებზე, მაგალითად, მტვრიან ოთახში ან ნისლის წვეთებში.
სად არის მნიშვნელოვანი იმის ცოდნა, თუ რა კუთხით ხვდება სხივი დაბრკოლებას?
არეკვლისა და რეფრაქციის ფენომენები არის ყველაზე ცნობილი ოპტიკური ეფექტები, რომლებსაც ადამიანი აწყდება ფაქტიურად ყოველდღე, როცა სარკეში საკუთარ თავს უყურებს ან სვამს ჭიქა ჩაის მასში მყოფი კოვზის დათვალიერების შემდეგ.
რეფრაქციისა და ასახვის მათემატიკური აღწერა მოითხოვს სხივის დაცემის კუთხის ცოდნას. მაგალითად, არეკვლის ფენომენს ახასიათებს არეკვლისა და დაცემის კუთხის თანასწორობა. თუ აღწერილია გარდატეხის პროცესის მხრიდან, დაცემის კუთხე და გარდატეხის კუთხე დაკავშირებულია ერთმანეთთან სინუსების ფუნქციებით და მედიის რეფრაქციული ინდექსებით (სნელის კანონი)..

კუთხე, რომლითაც სინათლის სხივი ეცემა ორ გამჭვირვალე მედიას შორის ინტერფეისზე, მნიშვნელოვან როლს ასრულებს ოპტიკურად უფრო მკვრივ მასალაში შიდა მთლიანი ასახვის ეფექტის განხილვისას. ეს ეფექტი შეინიშნება მხოლოდ დაცემის კუთხეების შემთხვევაში, რომლებიც აღემატება ზოგიერთ კრიტიკულ მნიშვნელობას.
განხილული კუთხის გეომეტრიული განსაზღვრება
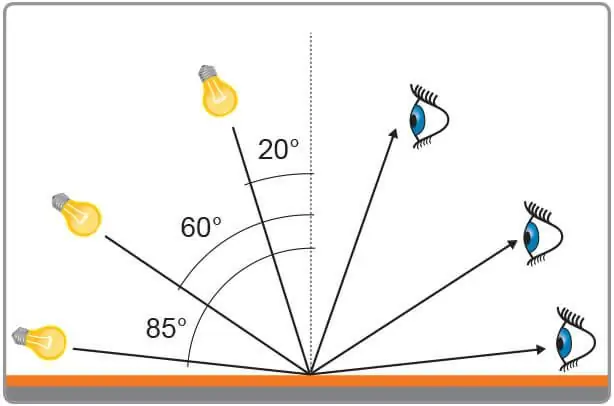
შეიძლება ვივარაუდოთ, რომ არის რაღაც ზედაპირი, რომელიც ჰყოფს ორ გარემოს. ეს ზედაპირი შეიძლება იყოს ბრტყელი, როგორც სარკის შემთხვევაში, ან შეიძლება იყოს უფრო რთული, მაგალითად, ზღვის ქედის ზედაპირი. წარმოიდგინეთ, რომ ამ ზედაპირზე მოდისსინათლის სხივი. როგორ განვსაზღვროთ სინათლის დაცემის კუთხე? ამის გაკეთება საკმაოდ მარტივია. ქვემოთ მოცემულია მოქმედებების თანმიმდევრობა, რომელიც უნდა გაკეთდეს სასურველი კუთხის მოსაძებნად.
- პირველ რიგში, თქვენ უნდა დაადგინოთ სხივის გადაკვეთის წერტილი ზედაპირთან.
- O-ს გავლით უნდა დახაზოთ განხილული ზედაპირის პერპენდიკულარული. მას ხშირად ნორმალურს უწოდებენ.
- სხივის დაცემის კუთხე ტოლია მასსა და ნორმას შორის კუთხის. მისი გაზომვა შესაძლებელია მარტივი პროტრაქტორით.
როგორც ხედავთ, განხილული კუთხის პოვნა არ არის რთული. თუმცა, მოსწავლეები ხშირად უშვებენ შეცდომას სიბრტყესა და სხივს შორის გაზომვისას. უნდა გვახსოვდეს, რომ დაცემის კუთხე ყოველთვის იზომება ნორმალურიდან, მიუხედავად ზედაპირის ფორმისა და საშუალებისა, რომელშიც ის ვრცელდება.
სფერული სარკეები, ლინზები და სხივები ეცემა მათზე
გარკვეული სხივების დაცემის კუთხეების თვისებების ცოდნა გამოიყენება სფერულ სარკეებსა და თხელ ლინზებში გამოსახულების აგებაში. ასეთი გამოსახულების შესაქმნელად საკმარისია ვიცოდეთ, თუ როგორ იქცევა ორი განსხვავებული სხივი დასახელებულ ოპტიკურ მოწყობილობებთან ურთიერთობისას. ამ სხივების კვეთა განსაზღვრავს გამოსახულების წერტილის პოზიციას. ზოგადად, ყოველთვის შეგიძლიათ იპოვოთ სამი განსხვავებული სხივი, რომელთა მიმდინარეობა ზუსტად არის ცნობილი (მესამე სხივი შეიძლება გამოყენებულ იქნას აგებული გამოსახულების სისწორის შესამოწმებლად). ეს სხივები დასახელებულია ქვემოთ.
- გადის მოწყობილობის მთავარი ოპტიკური ღერძის პარალელურად. ის გადის ფოკუსში ასახვის ან გარდატეხის შემდეგ.
- სხივი, რომელიც გადის მოწყობილობის ფოკუსში. ის ყოველთვის ასახავსგარდატეხა ძირითადი ღერძის პარალელურად.
- გავლა ოპტიკური ცენტრის გავლით (სფერული სარკესთვის ის ემთხვევა სფეროს ცენტრს, ლინზებისთვის - მის შიგნით). ასეთი სხივი არ ცვლის თავის ტრაექტორიას.
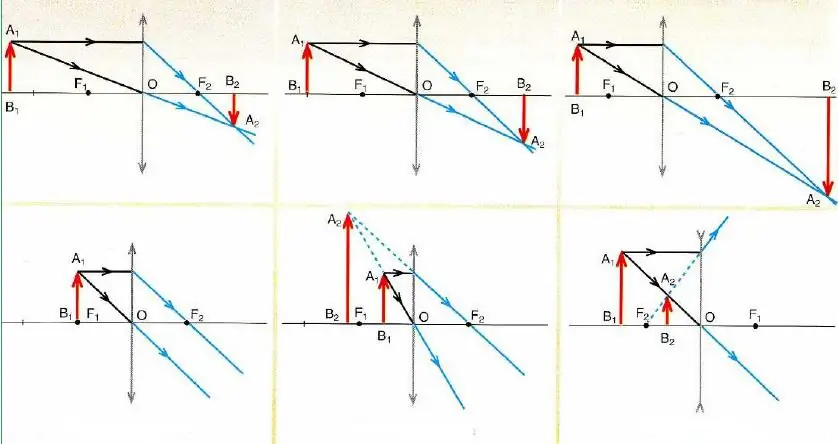
ზემოთ ფიგურაში ნაჩვენებია სურათების აგების სქემები სხვადასხვა ვარიანტებისთვის ობიექტის მდებარეობისთვის თხელ ლინზებთან მიმართებაში.






