ტიციუს-ბოდეს წესი (ზოგჯერ უბრალოდ ბოდეს კანონს უწოდებენ) არის ჰიპოთეზა, რომ სხეულები ზოგიერთ ორბიტალურ სისტემაში, მზის ჩათვლით, ბრუნავს ნახევრად ღერძების გასწვრივ, პლანეტარული მიმდევრობის მიხედვით. ფორმულა ვარაუდობს, რომ გარედან გაშლილი თითოეული პლანეტა მზიდან დაახლოებით ორჯერ უფრო დაშორებული იქნება, ვიდრე წინა.
ჰიპოთეზამ სწორად იწინასწარმეტყველა ცერესის (ასტეროიდების სარტყელში) და ურანის ორბიტა, მაგრამ ვერ დაადგინა ნეპტუნის ორბიტა და საბოლოოდ ჩაანაცვლა მზის სისტემის ფორმირების თეორიამ. მას ეწოდა იოჰან დანიელ ტიციუსისა და იოჰან ელერტ ბოდეს სახელი.

წარმოშობა
ბოდეს კანონის მიახლოების სერიის პირველი ნახსენები გვხვდება დევიდ გრიგორის ასტრონომიის ელემენტებში, რომელიც გამოქვეყნდა 1715 წელს. მასში ის ამბობს: „… თუ ვივარაუდებთ, რომ მანძილი მზიდან დედამიწამდე დაყოფილია ათ თანაბარ ნაწილად, რომელთაგან მერკურის მანძილი იქნება დაახლოებით ოთხი, ვენერადან შვიდი, მარსიდან თხუთმეტი, იუპიტერიდან ორმოცდათორმეტი. და სატურნიდან ოთხმოცდათხუთმეტიმსგავსი წინადადება, სავარაუდოდ, გრიგოლის შთაგონებით, ჩანს კრისტიან ვოლფის მიერ 1724 წელს გამოქვეყნებულ ნაშრომში.
1764 წელს ჩარლზ ბონეტმა თავის წიგნში „ბუნების ჭვრეტა“თქვა: „ჩვენ ვიცით ჩვიდმეტი პლანეტა, რომლებიც ქმნიან ჩვენს მზის სისტემას [ეს არის მთავარი პლანეტები და მათი თანამგზავრები], მაგრამ ჩვენ არ ვართ დარწმუნებული, რომ ისინი აღარ არიან." ამას, ბონეს ნაწარმოების 1766 წელს თარგმანში, იოჰან დანიელ ტიციუსმა დაამატა ორი აბზაცი მე-7 გვერდის ბოლოში და მე-8 გვერდის ზედა ნაწილში. ახალი ინტერპოლირებული აბზაცი არ არის ნაპოვნი ბონეს ორიგინალურ ტექსტში: არც იტალიურში. არც ნაწარმოების ინგლისური თარგმანები.
ტიციუსის აღმოჩენა
ტიციუსის ინტერკალურ ტექსტში ორი ნაწილია. პირველი ხსნის მზიდან პლანეტების დაშორების თანმიმდევრობას. ის ასევე შეიცავს რამდენიმე სიტყვას მზიდან იუპიტერამდე მანძილის შესახებ. მაგრამ ეს არ არის ტექსტის დასასრული.
ღირს რამდენიმე სიტყვის თქმა ტიციუს-ბოდეს წესის ფორმულაზე. ყურადღება მიაქციეთ პლანეტებს შორის დისტანციებს და გაარკვიეთ, რომ თითქმის ყველა მათგანი გამოყოფილია ერთმანეთისგან სხეულის ზომების შესაბამისი პროპორციით. მზიდან სატურნამდე მანძილი გაყავით 100 ნაწილად; მაშინ მერკური მზისგან ოთხი ასეთი ნაწილით არის გამოყოფილი; ვენერა - 4 + 3=7 ასეთ ნაწილად; დედამიწა - 4+6=10-ით; მარსი - 4+12=16-ით.
მაგრამ გაითვალისწინეთ, რომ მარსიდან იუპიტერამდე არის გადახრა ამ ასე ზუსტი პროგრესიიდან. 4+24=28 ასეთი ნაწილის სივრცე მოჰყვება მარსს, მაგრამ ჯერჯერობით იქ არც ერთი პლანეტა არ არის აღმოჩენილი. მაგრამ ლორდ არქიტექტორმა უნდა დატოვოს ეს ადგილი ცარიელი? არასოდეს. Ისედავუშვათ, რომ ეს სივრცე უეჭველად ეკუთვნის მარსის ჯერ კიდევ აღმოუჩენელ მთვარეებს და დავამატოთ, რომ შესაძლოა იუპიტერს ჯერ კიდევ ჰქონდეს რამდენიმე პატარა თანამგზავრი მის გარშემო, რომლებიც ჯერ არ უნახავთ არცერთ ტელესკოპს.

Bode-ის აღზევება
1772 წელს იოჰან ელერტ ბოდემ, ოცდახუთი წლის ასაკში, დაასრულა თავისი ასტრონომიული კრებულის Anleitung zur Kenntniss des gestirnten Himmels ("ვარსკვლავური ცის ცოდნის გზამკვლევი") მეორე გამოცემა. დაამატა შემდეგი სქოლიო, თავდაპირველად წყაროს გარეშე, მაგრამ აღნიშნულია შემდგომ ვერსიებში. ბოდეს მემუარებში შეიძლება მოიძებნოს ტიციუსის ცნობა მისი ავტორიტეტის აშკარა აღიარებით.

Opinion Bode
ასე ჟღერს ტიციუს-ბოდეს წესი ამ უკანასკნელის წარმოდგენისას: თუ მზიდან სატურნამდე მანძილი 100-ის ტოლია, მაშინ მერკური მზიდან გამოყოფილია ოთხი ასეთი ნაწილით. ვენერა - 4+3=7. დედამიწა - 4+6=10. მარსი - 4+12=16.
ახლა არის უფსკრული ამ მოწესრიგებულ პროგრესში. მარსის შემდეგ მოჰყვება სივრცე 4+24=28 გაანგარიშებით, რომელშიც ჯერ არც ერთი პლანეტა არ ჩანს. შეგვიძლია დავიჯეროთ, რომ სამყაროს დამფუძნებელმა ეს სივრცე ცარიელი დატოვა? Რათქმაუნდა არა. აქედან მივდივართ იუპიტერის დაშორებამდე 4+48=52 გაანგარიშების სახით და ბოლოს სატურნის მანძილამდე - 4+96=100.

ეს ორი განცხადება ყველა სპეციფიკურ ტიპოლოგიასა და ორბიტალურ რადიუსებთან დაკავშირებით, როგორც ჩანს, უძველესი დროიდან მოდის.ასტრონომია. ამ თეორიებიდან ბევრი თარიღდება მეჩვიდმეტე საუკუნემდე.
გავლენა
ტიციუსი იყო გერმანელი ფილოსოფოსის კრისტიან ფრეიჰერ ფონ ვოლფის (1679-1754) სტუდენტი. ბონეს ნაშრომში ჩასმული ტექსტის მეორე ნაწილი ეფუძნება ფონ ვოლფის 1723 წლის ნაშრომს Vernünftige Gedanken von den Wirkungen der Natur..
მეოცე საუკუნის ლიტერატურა ტიციუს-ბოდეს წესის ავტორობას გერმანელ ფილოსოფოსს ანიჭებს. თუ ასეა, ტიციუსს შეეძლო მისგან სწავლა. კიდევ ერთი ძველი ცნობა დაწერა ჯეიმს გრეგორმა 1702 წელს თავის Astronomiae Physicae et geometryae Elementa-ში, სადაც პლანეტების დისტანციების 4, 7, 10, 16, 52 და 100 თანმიმდევრობა გახდა 2 თანაფარდობის გეომეტრიული პროგრესია.
ეს არის ნიუტონის უახლოესი ფორმულა და ასევე ნაპოვნი იქნა ბენჯამინ მარტინისა და თომას სეარდის ნაწერებში, ბონეტის წიგნის გერმანიაში გამოქვეყნებამდე წლებით ადრე.
შემდეგი სამუშაო და პრაქტიკული შედეგები
ტიციუსი და ბოდე იმედოვნებდნენ, რომ კანონი გამოიწვევდა ახალი პლანეტების აღმოჩენას და მართლაც, ურანისა და ცერესის აღმოჩენამ, რომელთა შორის მანძილი კარგად ეთანხმება კანონს, ხელი შეუწყო მის მიღებას მეცნიერული სამყაროს მიერ.
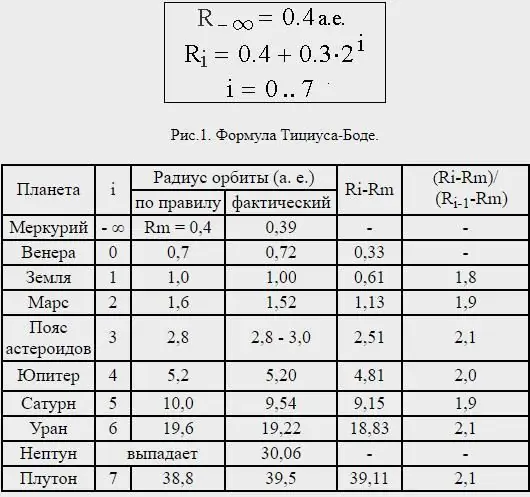
თუმცა, ნეპტუნის მანძილი ძალიან არათანმიმდევრული იყო, და სინამდვილეში პლუტონი - ახლა პლანეტად არ ითვლება - არის საშუალო მანძილით, რომელიც დაახლოებით შეესაბამება ტიციუს-ბოდეს კანონს, რომელიც იწინასწარმეტყველეს ურანის გარეთ შემდეგი პლანეტისთვის.
თავდაპირველად გამოქვეყნებულ კანონს დაახლოებით აკმაყოფილებდა ყველა ცნობილი პლანეტა - მერკური და სატურნი - შორის არსებული უფსკრულით.მეოთხე და მეხუთე პლანეტები. ეს ითვლებოდა საინტერესო, მაგრამ არა დიდი მნიშვნელობის ფიგურად 1781 წელს ურანის აღმოჩენამდე, რომელიც ჯდება სერიაში.
ამ აღმოჩენის საფუძველზე, ბოდემ მოუწოდა მეხუთე პლანეტის ძებნას. ცერერა, ყველაზე დიდი ობიექტი ასტეროიდთა სარტყელში, აღმოაჩინეს ბოდეს წინასწარმეტყველურ პოზიციაზე 1801 წელს. ბოდეს კანონი ფართოდ იყო მიღებული მანამ, სანამ ნეპტუნი არ იქნა აღმოჩენილი 1846 წელს და აჩვენეს, რომ იგი არ შეესაბამება კანონს.
ამავდროულად, სარტყელში აღმოჩენილი ასტეროიდების დიდმა რაოდენობამ ცერერა პლანეტების სიიდან გადალახა. ბოდეს კანონი განიხილა ასტრონომმა და ლოგიკოსმა ჩარლზ სანდერს პირსმა 1898 წელს, როგორც მცდარი მსჯელობის მაგალითი.

პრობლემის განვითარება
1930 წელს პლუტონის აღმოჩენამ კიდევ უფრო გაართულა პრობლემა. მიუხედავად იმისა, რომ ის არ ემთხვეოდა ბოდეს კანონით ნაწინასწარმეტყველებულ პოზიციას, ის ეხებოდა იმ პოზიციას, რომელიც კანონმა იწინასწარმეტყველა ნეპტუნისთვის. თუმცა, კოიპერის სარტყლის შემდგომმა აღმოჩენამ და, კერძოდ, ობიექტის ერისი, რომელიც პლუტონზე უფრო მასიურია, მაგრამ არ შეესაბამება ბოდეს კანონს, კიდევ უფრო დისკრედიტაცია მოახდინა ფორმულაზე..
სერდას წვლილი
იეზუიტმა თომას სერდამ ჩაატარა ცნობილი ასტრონომიის კურსი ბარსელონაში 1760 წელს, მათემატიკის სამეფო კათედრაზე Sant Jaume de Cordelle-ის კოლეჯში (კორდელის დიდებულთა იმპერიული და სამეფო სემინარია). სერდასის ტრატადოში ჩნდება პლანეტარული დისტანციები, მიღებული კეპლერის მესამე კანონის გამოყენებით, 10-3 სიზუსტით..
თუ ავიღებთ 10-ად დედამიწიდან დაშორებას დადამრგვალება მთელ რიცხვამდე, გეომეტრიული პროგრესია [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, n=2-დან n=8-მდე, შეიძლება იყოს გამოხატული. და კეპლერის ანომალიის წრიული ერთგვაროვანი ფიქტიური მოძრაობის გამოყენებით, Rn მნიშვნელობები, რომლებიც შეესაბამება თითოეული პლანეტის შეფარდებას, შეიძლება მივიღოთ, როგორც rn=(Rn - R1) / (Rn-1 - R1), რის შედეგადაც არის 1.82; 1, 84; 1, 86; 1.88 და 1.90, სადაც rn=2 - 0.02 (12 - n) არის აშკარა კავშირი კეპლერის უწყვეტობასა და ტიციუს-ბოდეს კანონს შორის, რომელიც ითვლება შემთხვევით რიცხვობრივ დამთხვევად. გამოთვლის შედეგი ორთან ახლოსაა, მაგრამ დუი შეიძლება ჩაითვალოს 1 რიცხვის დამრგვალებად, 82.

პლანეტის საშუალო სიჩქარე n=1-დან n=8-მდე ამცირებს მზიდან დაშორებას და განსხვავდება ერთგვაროვანი დაცემისგან n=2-ზე, რათა აღდგეს n=7-დან (ორბიტალური რეზონანსი). ეს გავლენას ახდენს მზიდან იუპიტერამდე დაშორებაზე. თუმცა, მანძილი ყველა სხვა ობიექტს შორის იმ ყბადაღებული წესის ფარგლებში, რომელსაც სტატია ეძღვნება, ასევე განისაზღვრება ამ მათემატიკური დინამიკით.
თეორიული ასპექტი
არ არსებობს მყარი თეორიული ახსნა, რომელიც საფუძვლად უდევს ტიციუს-ბოდეს წესს, მაგრამ შესაძლებელია, რომ ორბიტალური რეზონანსისა და თავისუფლების ხარისხის არარსებობის კომბინაციის გათვალისწინებით, ნებისმიერ სტაბილურ პლანეტურ სისტემას აქვს მაღალი ალბათობა გაიმეოროს აღწერილი მოდელი. ეს თეორია ორი მეცნიერის მიერ.
იმის გამო, რომ ეს შეიძლება იყოს მათემატიკური დამთხვევა და არა "ბუნების კანონი", მას ზოგჯერ წესს უწოდებენ და არა "კანონს". თუმცა, ასტროფიზიკოსი ალან ბოსი ამტკიცებს, რომ ეს უბრალოდდამთხვევა და პლანეტარული მეცნიერების ჟურნალი Icarus აღარ იღებს სტატიებს, რომლებიც ცდილობს „კანონის“გაუმჯობესებული ვერსიების მიწოდებას.
ორბიტალური რეზონანსი
ორბიტალური რეზონანსი ძირითადი ორბიტული სხეულებიდან ქმნის უბნებს მზის გარშემო, რომლებსაც არ აქვთ გრძელვადიანი სტაბილური ორბიტები. პლანეტების ფორმირების სიმულაციის შედეგები მხარს უჭერს აზრს, რომ შემთხვევით არჩეული სტაბილური პლანეტარული სისტემა, სავარაუდოდ, დააკმაყოფილებს ტიციუს-ბოდეს წესს.

დუბრული და გრანერი
დუბრულმა და გრანერმა აჩვენეს, რომ ძალაუფლების კანონის მანძილის წესები შეიძლება იყოს პლანეტარული სისტემების კოლაფსირებული ღრუბლების მოდელების შედეგი, რომლებსაც აქვთ ორი სიმეტრია: ბრუნვის უცვლელობა (ღრუბელი და მისი შიგთავსი ღერძის სიმეტრიულია) და მასშტაბის უცვლელობა (ღრუბელი და მისი შინაარსი ყველა მასშტაბით ერთნაირად გამოიყურება).
ეს უკანასკნელი არის მრავალი ფენომენის მახასიათებელი, რომელიც ფიქრობენ, რომ როლს თამაშობს პლანეტების ფორმირებაში, როგორიცაა ტურბულენტობა. მანძილი მზიდან მზის სისტემის პლანეტებამდე, შემოთავაზებული ტიციუსისა და ბოდეს მიერ, არ იქნა გადახედული დუბრულისა და გრანერის კვლევების ფარგლებში.






