თერმოდინამიკის მნიშვნელოვანი განყოფილება არის ნივთიერების სხვადასხვა ფაზებს შორის გარდაქმნების შესწავლა, ვინაიდან ეს პროცესები ხდება პრაქტიკაში და აქვს ფუნდამენტური მნიშვნელობა გარკვეული პირობების პირობებში სისტემის ქცევის პროგნოზირებისთვის. ამ გარდაქმნებს უწოდებენ ფაზურ გადასვლებს, რომლებსაც ეძღვნება სტატია.
ფაზის და სისტემის კომპონენტის კონცეფცია

სანამ ფიზიკაში ფაზური გადასვლების განხილვის დაწყებამდე აუცილებელია განვსაზღვროთ თავად ფაზის ცნება. როგორც ზოგადი ფიზიკის კურსიდან არის ცნობილი, მატერიის სამი მდგომარეობაა: აირისებრი, მყარი და თხევადი. მეცნიერების სპეციალურ განყოფილებაში - თერმოდინამიკაში - კანონები ჩამოყალიბებულია მატერიის ფაზებისთვის და არა მათი აგრეგაციის მდგომარეობებისთვის. ფაზა გაგებულია, როგორც მატერიის გარკვეული მოცულობა, რომელსაც აქვს ერთგვაროვანი სტრუქტურა, ხასიათდება სპეციფიკური ფიზიკური და ქიმიური თვისებებით და დანარჩენი მატერიისგან გამოყოფილია საზღვრებით, რომლებსაც ინტერფაზა ეწოდება.
ამგვარად, "ფაზის" კონცეფცია შეიცავს ბევრად უფრო მნიშვნელოვან ინფორმაციას თვისებების შესახებ.მატერია, ვიდრე მისი აგრეგაციის მდგომარეობა. მაგალითად, ლითონის მყარი მდგომარეობა, როგორიცაა რკინა, შეიძლება იყოს შემდეგ ფაზებში: დაბალი ტემპერატურის მაგნიტური სხეულზე ორიენტირებული კუბური (BCC), დაბალი ტემპერატურის არამაგნიტური bcc, სახეზე ორიენტირებული კუბური (fcc) და მაღალი ტემპერატურა. ტემპერატურა არამაგნიტური წკ.
„ფაზის“ცნების გარდა, თერმოდინამიკის კანონებში ასევე გამოიყენება ტერმინი „კომპონენტები“, რაც ნიშნავს ქიმიური ელემენტების რაოდენობას, რომლებიც ქმნიან კონკრეტულ სისტემას. ეს ნიშნავს, რომ ფაზა შეიძლება იყოს მონოკომპონენტიანი (1 ქიმიური ელემენტი) ან მრავალკომპონენტიანი (რამდენიმე ქიმიური ელემენტი).
გიბსის თეორემა და წონასწორობა სისტემის ფაზებს შორის

ფაზური გადასვლების გასაგებად, აუცილებელია ვიცოდეთ მათ შორის წონასწორობის პირობები. ეს პირობები შეიძლება მათემატიკურად მივიღოთ გიბსის განტოლებების სისტემის ამოხსნით თითოეული მათგანისთვის, თუ ვივარაუდებთ, რომ წონასწორობის მდგომარეობა მიიღწევა მაშინ, როდესაც გარე გავლენისგან იზოლირებული სისტემის ჯამური გიბსის ენერგია შეწყვეტს ცვლილებას.
განტოლებათა მითითებული სისტემის ამოხსნის შედეგად მიიღება რამდენიმე ფაზას შორის წონასწორობის არსებობის პირობები: იზოლირებული სისტემა შეწყვეტს განვითარებას მხოლოდ მაშინ, როცა თითოეული კომპონენტის წნევა, ქიმიური პოტენციალი და ტემპერატურა ყველა ფაზაში. ერთმანეთის ტოლია.
გიბსის ფაზის წესი წონასწორობისთვის

სისტემა, რომელიც შედგება რამდენიმე ფაზისა და კომპონენტისგან, შეიძლება იყოს წონასწორობაში არა მხოლოდგარკვეულ პირობებში, მაგალითად, სპეციფიკურ ტემპერატურასა და წნევაზე. წონასწორობისთვის გიბსის თეორემის ზოგიერთი ცვლადი შეიძლება შეიცვალოს ამ წონასწორობაში მყოფი ფაზების და კომპონენტების რაოდენობის შენარჩუნებით. ცვლადების რაოდენობას, რომლებიც შეიძლება შეიცვალოს სისტემაში წონასწორობის დარღვევის გარეშე, ეწოდება ამ სისტემის თავისუფლებების რაოდენობას.
f ფაზებისა და k კომპონენტებისგან შემდგარი სისტემის l თავისუფლებების რაოდენობა ცალსახად განისაზღვრება გიბსის ფაზის წესიდან. ეს წესი მათემატიკურად იწერება შემდეგნაირად: l + f=k + 2. როგორ ვიმუშაოთ ამ წესთან? Ძალიან მარტივი. მაგალითად, ცნობილია, რომ სისტემა შედგება f=3 წონასწორობის ფაზისაგან. რა არის კომპონენტების მინიმალური რაოდენობა, რომელიც შეიძლება შეიცავდეს ასეთ სისტემას? თქვენ შეგიძლიათ უპასუხოთ კითხვას შემდეგი მსჯელობით: წონასწორობის შემთხვევაში, ყველაზე მკაცრი პირობები არსებობს, როდესაც ის რეალიზდება მხოლოდ გარკვეულ ინდიკატორებზე, ანუ ნებისმიერი თერმოდინამიკური პარამეტრის ცვლილება გამოიწვევს დისბალანსს. ეს ნიშნავს, რომ თავისუფლებების რაოდენობა l=0. l და f-ის ცნობილი მნიშვნელობების ჩანაცვლებით ვიღებთ k=1, ანუ სისტემა, რომელშიც სამი ფაზა წონასწორობაშია, შეიძლება შედგებოდეს ერთი კომპონენტისგან. მთავარი მაგალითია წყლის სამმაგი წერტილი, სადაც ყინული, თხევადი წყალი და ორთქლი წონასწორობაშია სპეციფიკურ ტემპერატურასა და წნევაზე.
ფაზური გარდაქმნების კლასიფიკაცია
თუ წონასწორობაში მყოფ სისტემაში დაიწყებთ ზოგიერთი თერმოდინამიკური პარამეტრის შეცვლას, შეგიძლიათ დააკვირდეთ, როგორ გაქრება ერთი ფაზა და გამოჩნდება მეორე. ამ პროცესის მარტივი მაგალითია ყინულის დნობა მისი გაცხელებისას.
იმის გათვალისწინებით, რომ გიბსის განტოლება დამოკიდებულია მხოლოდ ორ ცვლადზე (წნევა და ტემპერატურა) და ფაზური გადასვლა მოიცავს ამ ცვლადების ცვლილებას, მაშინ მათემატიკურად ფაზებს შორის გადასვლა შეიძლება აღწერილი იყოს გიბსის ენერგიის დიფერენცირებით მის მიმართ. ცვლადები. სწორედ ეს მიდგომა გამოიყენა ავსტრიელმა ფიზიკოსმა პოლ ერენფესტმა 1933 წელს, როდესაც მან შეადგინა ყველა ცნობილი თერმოდინამიკური პროცესის კლასიფიკაცია, რომელიც ხდება ფაზის წონასწორობის ცვლილებით.
თერმოდინამიკის საფუძვლებიდან გამომდინარეობს, რომ გიბსის ენერგიის პირველი წარმოებული ტემპერატურის მიმართ უდრის სისტემის ენტროპიის ცვლილებას. გიბსის ენერგიის წარმოებული წნევის მიმართ უდრის მოცულობის ცვლილებას. თუ, როდესაც სისტემაში ფაზები იცვლება, ენტროპია ან მოცულობა განიცდის რღვევას, ანუ ისინი მკვეთრად იცვლება, მაშინ ისინი საუბრობენ პირველი რიგის ფაზის გადასვლაზე.
შემდეგ, გიბსის ენერგიის მეორე წარმოებულები ტემპერატურისა და წნევის მიმართ არის სითბოს სიმძლავრე და მოცულობითი გაფართოების კოეფიციენტი, შესაბამისად. თუ ფაზებს შორის ტრანსფორმაციას თან ახლავს მითითებული ფიზიკური სიდიდეების მნიშვნელობების შეწყვეტა, მაშინ საუბარია მეორე რიგის ფაზის გადასვლაზე.
ფაზებს შორის გარდაქმნების მაგალითები

ბუნებაში არის უზარმაზარი რაოდენობის სხვადასხვა გადასვლები. ამ კლასიფიკაციის ფარგლებში, პირველი სახის გადასვლების თვალსაჩინო მაგალითებია ლითონების დნობის ან ჰაერიდან წყლის ორთქლის კონდენსაციის პროცესები, როდესაც სისტემაში ხდება მოცულობის ნახტომი.
თუ ვსაუბრობთ მეორე რიგის გადასვლებზე, მაშინ ნათელი მაგალითებია რკინის ტრანსფორმაცია მაგნიტურიდან პარამაგნიტურ მდგომარეობაში ტემპერატურაზე.768 ºC ან მეტალის გამტარის გადაქცევა ზეგამტარ მდგომარეობაში ტემპერატურაზე აბსოლუტურ ნულთან ახლოს.
განტოლებები, რომლებიც აღწერს პირველი სახის გადასვლებს
პრაქტიკაში ხშირად საჭიროა ვიცოდეთ, თუ როგორ იცვლება ტემპერატურა, წნევა და აბსორბირებული (გამოთავისუფლებული) ენერგია სისტემაში, როდესაც მასში ხდება ფაზური გარდაქმნები. ამ მიზნით გამოიყენება ორი მნიშვნელოვანი განტოლება. ისინი მიიღება თერმოდინამიკის საფუძვლების ცოდნის საფუძველზე:
- კლაპეირონის ფორმულა, რომელიც ადგენს ურთიერთობას წნევასა და ტემპერატურას შორის სხვადასხვა ფაზებს შორის ტრანსფორმაციის დროს.
- კლაუზიუსის ფორმულა, რომელიც აკავშირებს შთანთქმის (გამოთავისუფლებულ) ენერგიას და სისტემის ტემპერატურას ტრანსფორმაციის დროს.
ორივე განტოლების გამოყენება ხდება არა მხოლოდ ფიზიკური სიდიდეების რაოდენობრივი დამოკიდებულების მისაღებად, არამედ წონასწორობის მრუდების დახრის ნიშნის განსაზღვრაში ფაზურ დიაგრამებზე.
განტოლება მეორე სახის გადასვლების აღწერისთვის

1-ლი და მე-2 ტიპის ფაზური გადასვლები აღწერილია სხვადასხვა განტოლებით, ვინაიდან კლაუზიუსის და კლაუზიუსის განტოლებების გამოყენება მეორე რიგის გადასვლებისთვის იწვევს მათემატიკურ გაურკვევლობას.
ამ უკანასკნელის აღსაწერად გამოყენებულია ერენფესტის განტოლებები, რომლებიც ადგენენ ურთიერთობას წნევისა და ტემპერატურის ცვლილებებს შორის ტრანსფორმაციის პროცესის დროს სითბოს სიმძლავრის და მოცულობითი გაფართოების კოეფიციენტის ცვლილებების ცოდნის მეშვეობით. ერენფესტის განტოლებები გამოიყენება გამტარ-ზეგამტარის გადასვლების აღსაწერად მაგნიტური ველის არარსებობის შემთხვევაში.
მნიშვნელობაფაზური დიაგრამები
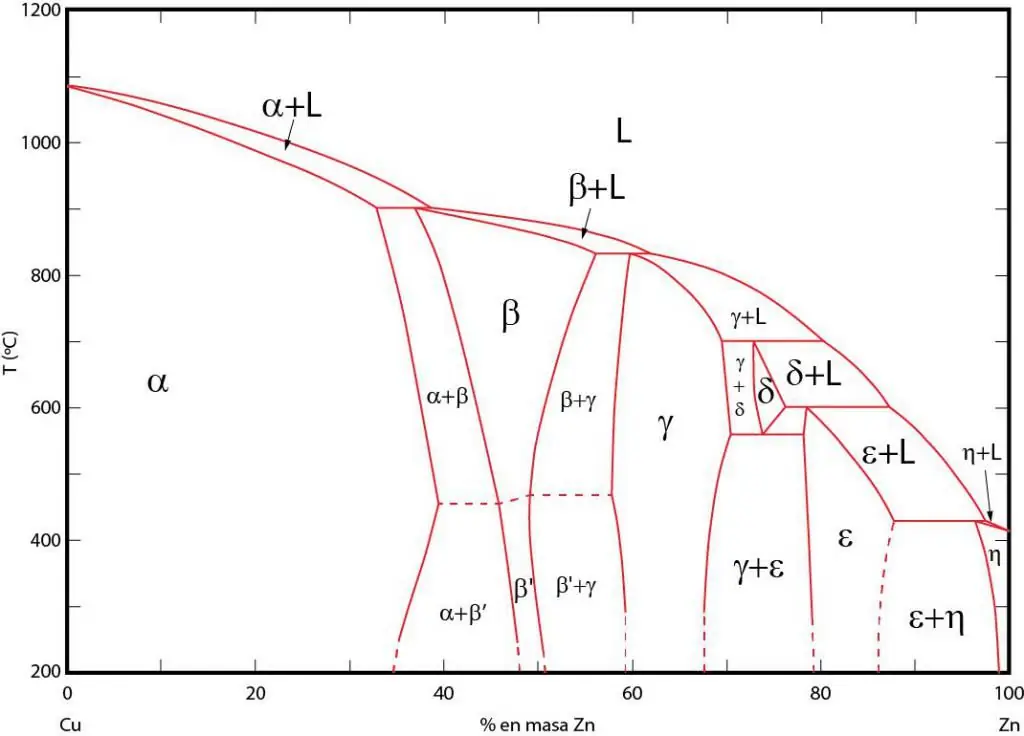
ფაზების დიაგრამები არის იმ უბნების გრაფიკული წარმოდგენა, რომლებშიც შესაბამისი ფაზები წონასწორობაშია. ეს ადგილები გამოყოფილია წონასწორობის ხაზებით ფაზებს შორის. ხშირად გამოიყენება P-T (წნევა-ტემპერატურა), T-V (ტემპერატურა-მოცულობა) და P-V (წნევა-მოცულობის) ფაზური დიაგრამები.
ფაზური დიაგრამების მნიშვნელობა მდგომარეობს იმაში, რომ ისინი საშუალებას გაძლევთ წინასწარ განსაზღვროთ რა ფაზაში იქნება სისტემა, როდესაც გარე პირობები შესაბამისად შეიცვლება. ეს ინფორმაცია გამოიყენება სხვადასხვა მასალის თერმული დამუშავებისას სასურველი თვისებების მქონე სტრუქტურის მისაღებად.






