არსებობენ ობიექტები, რომლებსაც შეუძლიათ შეცვალონ მათზე მოხვედრილი ელექტრომაგნიტური გამოსხივების ნაკადის სიმკვრივე, ანუ გაზარდონ იგი ერთ წერტილში შეგროვებით, ან შეამცირონ მისი გაფანტვით. ამ ობიექტებს ფიზიკაში ლინზები ეწოდება. მოდით უფრო ახლოს მივხედოთ ამ საკითხს.
რა არის ლინზები ფიზიკაში?
ეს კონცეფცია ნიშნავს აბსოლუტურად ნებისმიერ ობიექტს, რომელსაც შეუძლია შეცვალოს ელექტრომაგნიტური გამოსხივების გავრცელების მიმართულება. ეს არის ლინზების ზოგადი განმარტება ფიზიკაში, რომელიც მოიცავს ოპტიკურ სათვალეებს, მაგნიტურ და გრავიტაციულ ლინზებს.
ამ სტატიაში ყურადღება გამახვილდება ოპტიკურ სათვალეებზე, რომლებიც არის გამჭვირვალე მასალისგან დამზადებული და ორი ზედაპირით შეზღუდული ობიექტები. ერთ-ერთ ამ ზედაპირს აუცილებლად უნდა ჰქონდეს გამრუდება (ანუ იყოს სასრული რადიუსის სფეროს ნაწილი), წინააღმდეგ შემთხვევაში ობიექტს არ ექნება სინათლის სხივების გავრცელების მიმართულების შეცვლის თვისება.
ლინზის პრინციპი

ამ გაურთულებელი მუშაობის არსიოპტიკური ობიექტი არის მზის სხივების გარდატეხის ფენომენი. XVII საუკუნის დასაწყისში ცნობილმა ჰოლანდიელმა ფიზიკოსმა და ასტრონომმა უილბრორდ სნელ ვან რუიენმა გამოაქვეყნა რეფრაქციის კანონი, რომელიც ამჟამად მის გვარს ატარებს. ამ კანონის ფორმულირება ასეთია: როდესაც მზის შუქი გადის ორ ოპტიკურად გამჭვირვალე მედიას შორის ინტერფეისში, მაშინ სხივს შორის დაცემის კუთხის სინუსის ნამრავლი და ზედაპირის მიმართ ნორმალურს და იმ გარემოს გარდატეხის ინდექსი, რომელშიც ის ავრცელებს არის მუდმივი მნიშვნელობა.

ზემოხსენებულის გასარკვევად მოვიყვანთ მაგალითს: დაეცემა სინათლე წყლის ზედაპირზე, ხოლო კუთხე ნორმალურ ზედაპირსა და სხივს შორის არის θ1. შემდეგ, სინათლის სხივი ირღვევა და იწყებს თავის გავრცელებას წყალში უკვე ზედაპირის მიმართ ნორმალური კუთხით θ2. სნელის კანონის მიხედვით, ვიღებთ: sin(θ1)n1=sin(θ2) n2, სადაც n1 და n2 არის ჰაერისა და წყლის რეფრაქციული მაჩვენებლები, შესაბამისად. რა არის რეფრაქციული ინდექსი? ეს არის მნიშვნელობა, რომელიც აჩვენებს რამდენჯერ აღემატება ელექტრომაგნიტური ტალღების გავრცელების სიჩქარეს ვაკუუმში, ვიდრე ოპტიკურად გამჭვირვალე გარემოსთვის, ანუ n=c/v, სადაც c და v არის სინათლის სიჩქარე ვაკუუმში და საშუალო, შესაბამისად.
რეფრაქციის გამოჩენის ფიზიკა ფერმას პრინციპის განხორციელებაში მდგომარეობს, რომლის მიხედვითაც სინათლე მოძრაობს ისე, რომ უმოკლეს დროში გადალახოს მანძილი ერთი წერტილიდან მეორემდე სივრცეში.
ლინზების ტიპები

ოპტიკური ლინზის ტიპი ფიზიკაში განისაზღვრება მხოლოდ ზედაპირის ფორმის მიხედვით, რომელიც ქმნის მას. მათზე მოხვედრილი სხივის გარდატეხის მიმართულება დამოკიდებულია ამ ფორმაზე. ასე რომ, თუ ზედაპირის გამრუდება დადებითია (ამოზნექილი), მაშინ ლინზიდან გამოსვლისას სინათლის სხივი უფრო ახლოს გავრცელდება მის ოპტიკურ ღერძთან (იხ. ქვემოთ). პირიქით, თუ ზედაპირის გამრუდება უარყოფითია (ჩაზნექილი), მაშინ ოპტიკურ მინაზე გავლისას სხივი თავის ცენტრალურ ღერძს შორდება.
კიდევ ერთხელ გაითვალისწინეთ, რომ ნებისმიერი მრუდის ზედაპირი ერთნაირად არღვევს სხივებს (სტელას კანონის მიხედვით), მაგრამ მათ ნორმალურს აქვს განსხვავებული დახრილობა ოპტიკურ ღერძთან მიმართებაში, რაც იწვევს გარდატეხილი სხივის განსხვავებულ ქცევას.
ორი ამოზნექილი ზედაპირით შემოსაზღვრულ ლინზს ეწოდება კონვერგირებადი ლინზა. თავის მხრივ, თუ იგი წარმოიქმნება უარყოფითი მრუდის მქონე ორი ზედაპირით, მაშინ მას გაფანტვა ეწოდება. ყველა სხვა ტიპის ოპტიკური სათვალე ასოცირდება ამ ზედაპირების კომბინაციასთან, რომელსაც ასევე ემატება თვითმფრინავი. რა თვისება ექნება კომბინირებულ ლინზას (განსხვავებული ან კონვერგენტული) დამოკიდებულია მისი ზედაპირის რადიუსების მთლიან გამრუდებაზე.
ლინზის ელემენტები და სხივების თვისებები

გამოსახულების ფიზიკაში ლინზების შესაქმნელად, თქვენ უნდა გაეცნოთ ამ ობიექტის ელემენტებს. ისინი ჩამოთვლილია ქვემოთ:
- მთავარი ოპტიკური ღერძი და ცენტრი. პირველ შემთხვევაში, ისინი გულისხმობენ სწორ ხაზს, რომელიც გადის ობიექტივზე პერპენდიკულარულად მისი ოპტიკური ცენტრის გავლით.ეს უკანასკნელი, თავის მხრივ, არის წერტილი ლინზის შიგნით, რომელიც გადის, რომლის მეშვეობითაც სხივი არ განიცდის გარდატეხას.
- ფოკუსური მანძილი და ფოკუსი - მანძილი ცენტრსა და ოპტიკური ღერძის წერტილს შორის, რომელიც აგროვებს ამ ღერძის პარალელურად ობიექტივზე მოხვედრილ ყველა სხივს. ეს განმარტება მართალია ოპტიკური სათვალეების შეგროვებისთვის. დივერგენციული ლინზების შემთხვევაში, ეს არ არის თვით სხივები, რომლებიც გადაიყრება წერტილამდე, არამედ მათი წარმოსახვითი გაგრძელება. ამ პუნქტს მთავარი აქცენტი ეწოდება.
- ოპტიკური სიმძლავრე. ეს არის ფოკუსური სიგრძის ორმხრივი სახელი, ანუ D \u003d 1 / f. იგი იზომება დიოპტრიებში (დიოპტრიაში), ანუ 1 დიოპტრიაში.=1 მ-1.
ქვემოთ მოცემულია სხივების ძირითადი თვისებები, რომლებიც გადის ლინზაში:
- სხივი, რომელიც გადის ოპტიკურ ცენტრში, არ ცვლის მოძრაობის მიმართულებას;
- სხივები იცვლის მიმართულებას ისე, რომ გაიაროს მთავარ ფოკუსში;
- სხივები, რომლებიც ეცემა ოპტიკურ მინაზე ნებისმიერი კუთხით, მაგრამ გადის მის ფოკუსში, იცვლის გავრცელების მიმართულებას ისე, რომ ხდება მთავარი ოპტიკური ღერძის პარალელურად.
მთავარი ოპტიკური ღერძის პარალელურად მოხვედრილი
სხივების ზემოაღნიშნული თვისებები წვრილი ლინზებისთვის ფიზიკაში (როგორც მათ უწოდებენ, რადგან არ აქვს მნიშვნელობა რა სფეროები წარმოიქმნება და რამდენად სქელია ისინი, მხოლოდ ობიექტის ოპტიკურ თვისებებს აქვს მნიშვნელობა) მათში გამოსახულების შესაქმნელად გამოიყენება..
გამოსახულებები ოპტიკურ სათვალეებში: როგორ ავაშენოთ?
ქვემოთ მოცემულია ფიგურა, რომელიც დეტალურადაა აღწერილი საგნის ამოზნექილ და ჩაზნექილ ლინზებში გამოსახულების აგების სქემებს(წითელი ისარი) მისი პოზიციიდან გამომდინარე.
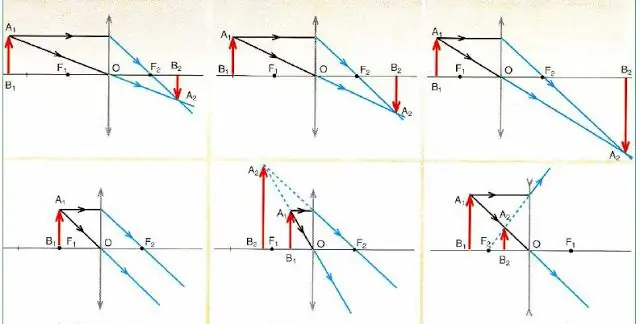
მნიშვნელოვანი დასკვნები გამომდინარეობს სქემების ანალიზიდან ნახატზე:
- ნებისმიერი გამოსახულება აგებულია მხოლოდ 2 სხივზე (გადის ცენტრში და ძირითადი ოპტიკური ღერძის პარალელურად).
- კონვერგირებულმა ლინზებმა (აღნიშნეს ისრებით ბოლოებზე მიმართული გარეთ) შეუძლია მოგცეთ როგორც გადიდებული, ისე შემცირებული გამოსახულება, რომელიც თავის მხრივ შეიძლება იყოს რეალური (რეალური) ან წარმოსახვითი.
- თუ ობიექტი ფოკუსირებულია, მაშინ ობიექტივი არ ქმნის მის გამოსახულებას (იხილეთ ქვედა დიაგრამა მარცხნივ სურათზე).
- გაფანტული ოპტიკური სათვალეები (აღნიშნავს ისრებით მის ბოლოებზე, რომლებიც მიმართულია შიგნით) ყოველთვის იძლევა შემცირებულ და ვირტუალურ გამოსახულებას ობიექტის პოზიციის მიუხედავად.
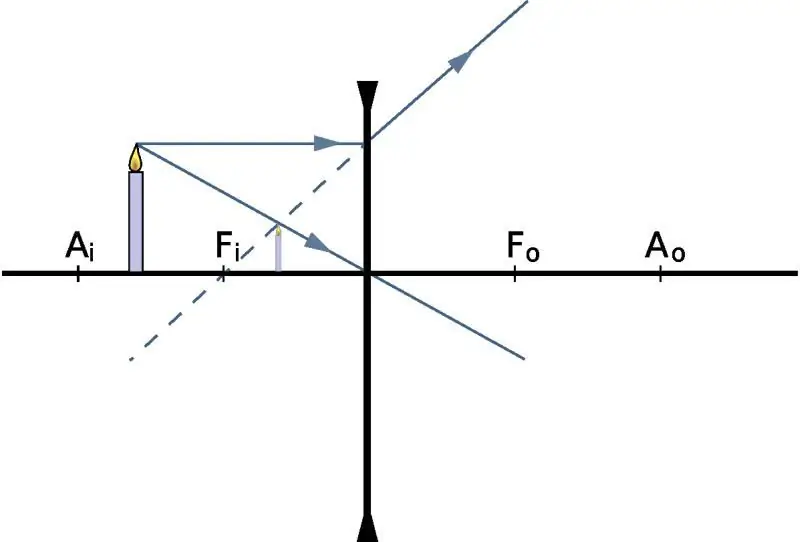
გამოსახულებამდე მანძილის პოვნა
იმისათვის, რომ განვსაზღვროთ რა მანძილზე გამოჩნდება გამოსახულება, თავად ობიექტის პოზიციის ცოდნით, ვაძლევთ ლინზის ფორმულას ფიზიკაში: 1/f=1/do + 1 /d i, სადაც do და di არის მანძილი ობიექტამდე და მის გამოსახულებამდე ოპტიკურიდან ცენტრი, შესაბამისად, f არის მთავარი აქცენტი. თუ ვსაუბრობთ შემგროვებელ ოპტიკურ მინაზე, მაშინ f- რიცხვი დადებითი იქნება. პირიქით, განსხვავებული ლინზებისთვის f არის უარყოფითი.
მოდით გამოვიყენოთ ეს ფორმულა და გადავწყვიტოთ მარტივი პრობლემა: დაე, ობიექტი იყოს დo=2f დაშორებით შემგროვებელი ოპტიკური მინის ცენტრიდან. სად გამოჩნდება მისი სურათი?
პრობლემის პირობიდან გვაქვს: 1/f=1/(2f)+1/di. საწყისი: 1/di=1/f - 1/(2f)=1/(2f), ანუ di=2 ვ. ამრიგად, გამოსახულება გამოჩნდება ობიექტივიდან ორი კერის მანძილზე, მაგრამ მეორე მხარეს, ვიდრე თავად ობიექტი (ეს მითითებულია di მნიშვნელობის დადებითი ნიშნით).
მოკლე ისტორია
საინტერესოა სიტყვა "ლინზის" ეტიმოლოგიის მიცემა. ის მომდინარეობს ლათინური სიტყვებიდან lens და lentis, რაც ნიშნავს "ოსპს", რადგან ოპტიკური ობიექტები მათი ფორმით ნამდვილად ჰგავს ამ მცენარის ნაყოფს.
სფერული გამჭვირვალე სხეულების გარდატეხის ძალა ცნობილი იყო ძველი რომაელებისთვის. ამ მიზნით იყენებდნენ წყლით სავსე მრგვალ მინის ჭურჭელს. თავად მინის ლინზების დამზადება მხოლოდ მე-13 საუკუნეში დაიწყო ევროპაში. მათ იყენებდნენ კითხვის ინსტრუმენტად (თანამედროვე სათვალე ან გამადიდებელი შუშა).
ოპტიკური ობიექტების აქტიური გამოყენება ტელესკოპების და მიკროსკოპების წარმოებაში თარიღდება მე-17 საუკუნით (ამ საუკუნის დასაწყისში გალილეომ გამოიგონა პირველი ტელესკოპი). გაითვალისწინეთ, რომ სტელას გარდატეხის კანონის მათემატიკური ფორმულირება, რომლის ცოდნის გარეშე შეუძლებელია სასურველი თვისებების მქონე ლინზების დამზადება, გამოქვეყნდა ჰოლანდიელი მეცნიერის მიერ იმავე მე-17 საუკუნის დასაწყისში.
სხვა ლინზები
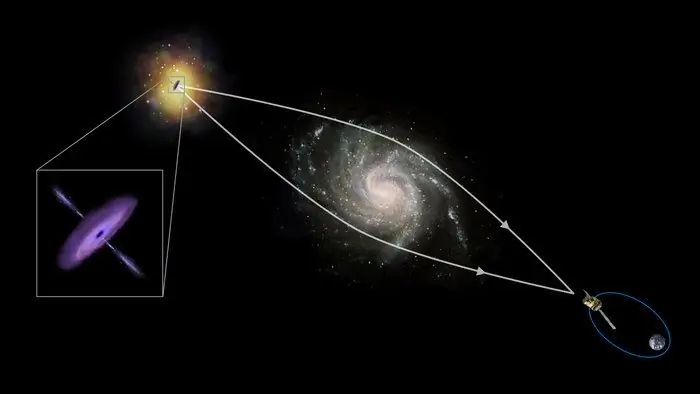
როგორც ზემოთ აღინიშნა, გარდა ოპტიკური რეფრაქციული ობიექტებისა, არსებობს აგრეთვე მაგნიტური და გრავიტაციული ობიექტები. პირველის მაგალითია მაგნიტური ლინზები ელექტრონულ მიკროსკოპში, ამ უკანასკნელის ნათელი მაგალითია სინათლის ნაკადის მიმართულების დამახინჯება,როდესაც ის გადის მასიურ კოსმოსურ სხეულებთან (ვარსკვლავები, პლანეტები).






