იმისთვის, რომ შეძლოთ ქაღალდზე ისეთი საგნების გამოსახვა, რომლებსაც რეალურად არც თუ ისე "მოხერხებული" ზომები აქვთ, ხალხმა მოიფიქრა მასშტაბი. სინამდვილეში, ეს ხსნის რისთვის არის განკუთვნილი სასწორი.
როდესაც სასკოლო სასწავლო გეგმა იწყებს მასშტაბის ცნების გამოვლენას
პირველად ბავშვები ხვდებიან ამ სიტყვას ტერიტორიის რუკებისა და გეგმების შესწავლისას. მასწავლებელი ახსნის, თუ რატომ არის საჭირო სასწორი, რას აჩვენებს იგი, მაგალითად ატლასების გამოყენებით. განმარტებულია, რომ ნებისმიერი გეოგრაფიული მახასიათებელი იმდენად დიდია, რომ მისი სრული ზომით გამოსახვა რთული და მოუხერხებელია.
ადამიანებმა რელიეფი დახატეს შემცირებული ფორმით, მაგრამ ამისთვის მათ არ გამოიყენეს ზუსტი თანაფარდობა. ახლა ეს უფრო ჭკვიანურად კეთდება - რუკაზე გამოსახულ თითოეულ ტირესა და ხაზს აქვს ზომა, რომელიც შეიძლება გამრავლდეს გარკვეულ რიცხვზე და გაირკვეს ნამდვილი სიგრძე და სიგანე.
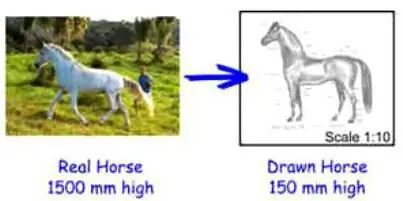
ჩანაწერის მასშტაბი: წაკითხვის პირველი გზა
სასწორი მითითებულია ორი რიცხვით, რომლებიც გამოყოფილია ორწერტილით. პირველი ციფრი მიუთითებს ფიგურაში განზომილების ერთეულებზე, მეორემიუთითებს ფიგურაში რამდენი რეალური ერთეული შეესაბამება პირველ რიცხვს. მაგალითად, თუ რომელიმე გეგმაზე მითითებულია 1:1000 მასშტაბი, ხოლო ზომების ერთეულები მითითებულია სანტიმეტრებში, მაშინ ფიგურაში ერთი სანტიმეტრი რეალურად შეესაბამება 1000 სმ. მაშ რისთვის არის სასწორი? მისი დახმარებით თქვენ შეგიძლიათ არა მხოლოდ შეამციროთ გარკვეული ობიექტები გრაფიკულ გეგმაზე, არამედ ზუსტად გამოთვალოთ მათი რეალური ზომა.
მასშტაბის ჩაწერის მეორე გზა: რა არის მოსახერხებელი?
მასშტაბის ორწერტით ჩაწერის წინა მეთოდს ეწოდება რიცხვითი. მაგრამ ასევე არსებობს დასახელებული მასშტაბი. მისი რეკორდი ასეთია: 1 სმ - 20 კმ. გამოდის, რომ ამ გზით შესაძლებელია კომპაქტურად ჩაიწეროს უზარმაზარი მასშტაბები, რომლებიც არ იქნება გამოხატული რიცხვებით რამდენიმე ნულით, თუ მოხდა სიტუაცია, როდესაც საჭიროა რამდენიმე ასეული კილომეტრის მითითება ერთ სანტიმეტრში. ამასთან, მაშინვე ირკვევა, რამდენი, რა და რაში. ეს ჩანაწერი უფრო ინტუიციური და ნათელია.
სკალირება ნახატში: რა ავსებს ადრე შესწავლილ კონცეფციას
მასშტაბის ცნება გვხვდება არა მხოლოდ გეოგრაფიაში, არამედ ისეთი საგნის შესწავლისას, როგორიცაა ნახატი. იგივე პრინციპები გამოიყენება სხვადასხვა ობიექტების გამოსახატავად. მაგრამ არის მნიშვნელოვანი განსხვავება: აქ კონცეფცია იმის შესახებ, თუ რა მასშტაბისთვის არის განკუთვნილი, ასევე გაფართოვდა იმით, რომ მისი გამოყენება შესაძლებელია მცირე დეტალების უფრო დიდი მასშტაბის გამოსახატავად. გეოგრაფიაში ამაზე არ ვსაუბრობთ, რადგან გეოგრაფიაში არ არის ისეთი პატარა ობიექტები, რომ მათი გაფართოების საჭიროება იყოს. კონტინენტები და მთები, მდინარეები და ტბები ნებისმიერ შემთხვევაში უფრო დიდია ვიდრე A4 ქაღალდის ფურცლები ან თუნდაცA1.
ნახატის შესწავლისას შეგიძლიათ გამოიყენოთ მასშტაბი, რათა უფრო დიდი სახით გამოსახოთ უმცირესი დეტალები, როგორიცაა ჭანჭიკი ან სამაგრი.
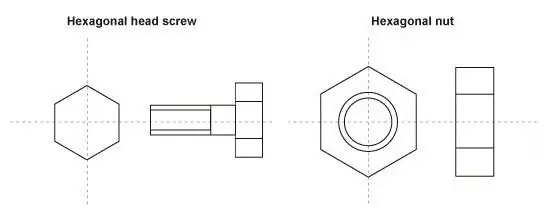
მაშ, რატომ გვჭირდება სასწორი ამ შემთხვევაში? მისი დახმარებით თქვენ შეგიძლიათ უფრო მოხერხებულად, ნათლად და დეტალურად გამოსახოთ პატარა ელემენტი. ამ შემთხვევაში, აღნიშვნაში ხდება საპირისპირო: პირველი რიცხვი მეორეზე მეტი იქნება, ხოლო აღნიშვნა 100:1 დაახლოებით ასე ჟღერს: სურათის 100 მეტრიკული ერთეული შეესაბამება რეალური ზომის ერთ ერთეულს.
რამდენიმე დამაზუსტებელი მაგალითი
რისთვის არის მასშტაბი, რას გვიჩვენებს პატარა ობიექტის გამოსახულების შემთხვევაში, რა შედეგია ქაღალდზე? ისევ გვაქვს ნაწილისა და რეალური ობიექტის გამოსახულების ზომების ზუსტი თანაფარდობა. გავიხსენოთ იგივე მასშტაბი 100:1. გამოდის, რომ ფიგურაში ასი მილიმეტრში არის მხოლოდ ერთი მილიმეტრი რეალური ზომა. თუ ნაწილის სიგანე სურათზე 500 მილიმეტრია, მისი რეალური სიგანე მხოლოდ 5 მილიმეტრია.
თუ გავიხსენებთ პირველ შემთხვევას, გამოსახულება დიდი ობიექტის პატარა ასლის ფურცელზე, მასშტაბი 1:100 ნიშნავს, რომ სურათზე ერთი მილიმეტრი შეიცავს 100 მილიმეტრს ნამდვილ ზომას. ასე რომ, თუ ობიექტის სიგრძე 80 მილიმეტრია ნახაზზე ან რუკაზე, ობიექტის რეალური სიგრძე იქნება 8000 მილიმეტრი. ნათელი მაგალითი იმისა, თუ რისთვის არის სასწორი და რა მოსახერხებელი გამოგონებაა კაცობრიობა.
სასწორის გამოყენებაში მთავარია დაუყოვნებლივგახსოვდეთ, რომ პირველი რიცხვი ეხება სურათს, ხოლო მეორე - ობიექტების რეალურ ზომას. იმისათვის, რომ მომავალში არ იყოს დაბნეული, ამ საფუძვლების გასამყარებლად, სკოლებში ტარდება პრაქტიკული მეცადინეობები გეოგრაფიაში, რათა ბავშვებმა ატლასის გამოყენებით რამდენჯერმე ახსნან და გამოთვალონ რეალური ობიექტების ზომები. იგივე ხდება ხატვის გაკვეთილებზე.
შეჯამება
რისთვის არის სასწორი? ამ კითხვაზე პასუხი შედგება სამი პუნქტისგან, რომელიც უბრალოდ უნდა გახსოვდეთ:
- პირველი - სასწორი აუცილებელია დიდი ობიექტების სანახავად მოსახერხებელ ზედაპირზე გამოსატანად.
- მეორე - სასწორი საჭიროა იმისათვის, რომ გამოსახოთ პატარა ობიექტები უფრო დიდ ზომებში.
- მესამე - სასწორი საჭიროა იმისათვის, რომ ზუსტად განვსაზღვროთ რეალური ობიექტის ზომა, მიუხედავად მისი საწყისი ზომისა, მცირე თუ დიდი.






