ყველა ადამიანი თავისი ცხოვრების განმავლობაში ხვდება სხეულებს, რომლებიც მატერიის სამი საერთო მდგომარეობიდან ერთ-ერთში არიან. აგრეგაციის ყველაზე მარტივი მდგომარეობა შესასწავლად არის გაზი. სტატიაში განვიხილავთ იდეალური გაზის კონცეფციას, მივცემთ სისტემის მდგომარეობის განტოლებას და ასევე ყურადღებას მივაქცევთ აბსოლუტური ტემპერატურის აღწერას.
მატერიის აირის მდგომარეობა
თითოეულ სტუდენტს აქვს კარგი წარმოდგენა იმის შესახებ, თუ რა მდგომარეობაზეა საუბარი, როდესაც ესმის სიტყვა "გაზი". ეს სიტყვა გაგებულია, როგორც სხეული, რომელსაც შეუძლია დაიკავოს მისთვის მიწოდებული ნებისმიერი მოცულობა. მას არ ძალუძს შეინარჩუნოს ფორმა, რადგან ვერ გაუძლებს ოდნავ გარეგნულ გავლენასაც კი. ასევე, გაზი არ ინარჩუნებს მოცულობას, რაც განასხვავებს მას არა მხოლოდ მყარი, არამედ სითხეებისაგან.
ისევე როგორც სითხე, გაზი არის თხევადი ნივთიერება. აირებში მყარი სხეულების მოძრაობის პროცესში ეს უკანასკნელი აფერხებს ამ მოძრაობას. მიღებულ ძალას ეწოდება წინააღმდეგობა. მისი ღირებულება დამოკიდებულიასხეულის სიჩქარე გაზში.
გაზების ძლიერი მაგალითებია ჰაერი, ბუნებრივი აირი, რომელიც გამოიყენება სახლების გასათბობად და სამზარეულოსთვის, ინერტული აირები (Ne, Ar) გამოიყენება სარეკლამო ნათების მილების შესავსებად ან გამოიყენება ინერტული (არააგრესიული, დამცავი) გარემოს შესაქმნელად შედუღებისას..
იდეალური გაზი
სანამ გაზის კანონების აღწერასა და მდგომარეობის განტოლებაზე გადახვიდეთ, კარგად უნდა გესმოდეთ კითხვა, რა არის იდეალური გაზი. ეს კონცეფცია დანერგილია მოლეკულურ კინეტიკური თეორიაში (MKT). იდეალური გაზი არის ნებისმიერი გაზი, რომელიც აკმაყოფილებს შემდეგ მახასიათებლებს:
- ნაწილაკები, რომლებიც მას ქმნიან, არ ურთიერთქმედებენ ერთმანეთთან, გარდა პირდაპირი მექანიკური შეჯახებისა.
- ნაწილაკების ჭურჭლის კედლებთან ან მათ შორის შეჯახების შედეგად მათი კინეტიკური ენერგია და იმპულსი შენარჩუნებულია, ანუ შეჯახება ითვლება აბსოლუტურად ელასტიურად.
- ნაწილაკებს არ აქვთ ზომები, მაგრამ აქვთ სასრული მასა, ანუ ისინი მსგავსია მატერიალური წერტილების.
ბუნებრივია, რომ ნებისმიერი გაზი არ არის იდეალური, არამედ რეალური. მიუხედავად ამისა, მრავალი პრაქტიკული პრობლემის გადასაჭრელად, ეს მიახლოებები საკმაოდ მართებულია და შეიძლება გამოყენებულ იქნას. არსებობს ზოგადი ემპირიული წესი, რომელიც ამბობს: მიუხედავად ქიმიური ბუნებისა, თუ გაზს აქვს ტემპერატურა ოთახის ტემპერატურაზე მაღალი და წნევა ატმოსფერული ან უფრო დაბალი, მაშინ ის შეიძლება ჩაითვალოს იდეალური მაღალი სიზუსტით და შეიძლება გამოყენებულ იქნას აღსაწერად. ის.მდგომარეობის იდეალური აირის განტოლების ფორმულა.
კლაპეირონ-მენდელეევის კანონი
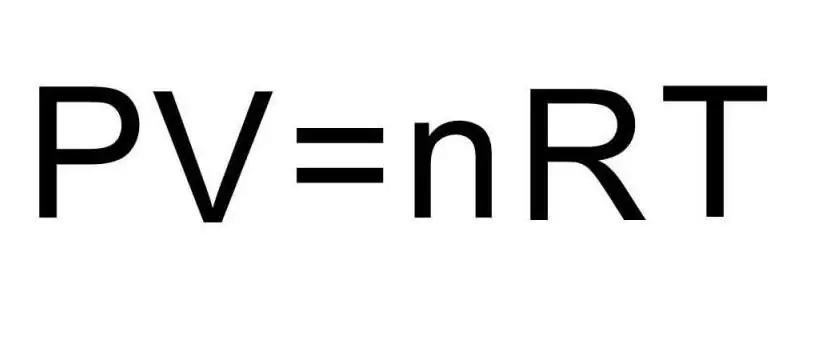
მატერიის სხვადასხვა აგრეგატურ მდგომარეობასა და პროცესებს შორის ერთიან აგრეგატურ მდგომარეობაში გადასვლები მკურნალობს თერმოდინამიკას. წნევა, ტემპერატურა და მოცულობა არის სამი სიდიდე, რომელიც ცალსახად განსაზღვრავს თერმოდინამიკური სისტემის ნებისმიერ მდგომარეობას. იდეალური აირის მდგომარეობის განტოლების ფორმულა აერთიანებს ამ სამივე რაოდენობას ერთ ტოლობაში. მოდით დავწეროთ ეს ფორმულა:
PV=nRT
აქ P, V, T - წნევა, მოცულობა, ტემპერატურა, შესაბამისად. n-ის მნიშვნელობა არის ნივთიერების რაოდენობა მოლებში, ხოლო სიმბოლო R აღნიშნავს აირების უნივერსალურ მუდმივას. ეს თანასწორობა გვიჩვენებს, რომ რაც მეტია წნევისა და მოცულობის ნამრავლი, მით მეტი უნდა იყოს ნივთიერებისა და ტემპერატურის ნამრავლი.

გაზის მდგომარეობის განტოლების ფორმულას ეწოდება კლაპეირონ-მენდელეევის კანონი. 1834 წელს ფრანგი მეცნიერი ემილ კლაპეირონი, თავისი წინამორბედების ექსპერიმენტული შედეგების შეჯამებით, მივიდა ამ განტოლებამდე. ამასთან, კლაპეირონმა გამოიყენა მთელი რიგი მუდმივები, რომლებიც მოგვიანებით მენდელეევმა შეცვალა ერთით - უნივერსალური გაზის მუდმივი R (8, 314 J / (molK)). ამიტომ, თანამედროვე ფიზიკაში ამ განტოლებას ფრანგი და რუსი მეცნიერების სახელები ჰქვია.

სხვა განტოლების ფორმები
ზემოთ, ჩვენ დავწერეთ მენდელეევ-კლაპეირონის მდგომარეობის განტოლება იდეალური გაზის საყოველთაოდ მიღებულ დამოსახერხებელი ფორმა. თუმცა, თერმოდინამიკის პრობლემებში ხშირად შეიძლება საჭირო გახდეს ოდნავ განსხვავებული ფორმა. ქვემოთ მოცემულია კიდევ სამი ფორმულა, რომლებიც პირდაპირ გამომდინარეობს დაწერილი განტოლებიდან:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
ეს სამი განტოლება ასევე უნივერსალურია იდეალური გაზისთვის, მხოლოდ მათში ჩანს ისეთი სიდიდეები, როგორიცაა m მასა, მოლური მასა M, სიმკვრივე ρ და N ნაწილაკების რაოდენობა, რომლებიც ქმნიან სისტემას. სიმბოლო kB აქ აღნიშნავს ბოლცმანის მუდმივას (1, 3810-23J/K).
ბოილ-მარიოტის კანონი
როდესაც კლაპეირონმა შეადგინა თავისი განტოლება, ის ეფუძნებოდა გაზის კანონებს, რომლებიც ექსპერიმენტულად აღმოაჩინეს რამდენიმე ათეული წლის წინ. ერთ-ერთი მათგანია ბოილ-მარიოტის კანონი. ის ასახავს იზოთერმულ პროცესს დახურულ სისტემაში, რის შედეგადაც იცვლება ისეთი მაკროსკოპული პარამეტრები, როგორიცაა წნევა და მოცულობა. თუ იდეალური აირის მდგომარეობის განტოლებაში ჩავსვამთ T და n მუდმივას, მაშინ აირის კანონი მიიღებს ფორმას:
P1V1=P2V 2
ეს არის ბოილ-მარიოტის კანონი, რომელიც ამბობს, რომ წნევის და მოცულობის პროდუქტი შენარჩუნებულია თვითნებური იზოთერმული პროცესის დროს. ამ შემთხვევაში, თავად P და V მნიშვნელობები იცვლება.
თუ გამოსახავთ P(V) ან V(P), მაშინ იზოთერმები იქნება ჰიპერბოლები.
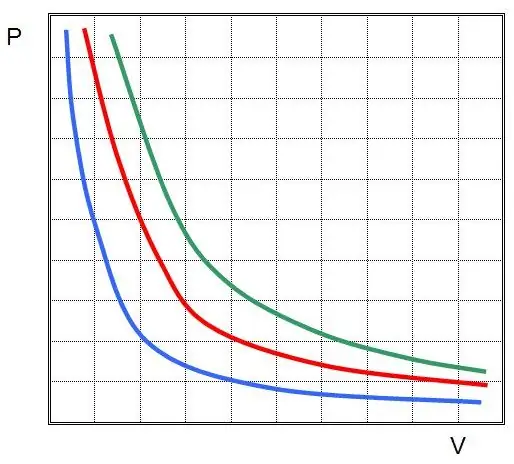
ჩარლზის და გეი-ლუსაკის კანონები
ეს კანონები მათემატიკურად აღწერს იზობარს და იზოქორიულსპროცესები, ანუ ისეთი გადასვლები გაზის სისტემის მდგომარეობებს შორის, რომლებშიც შენარჩუნებულია შესაბამისად წნევა და მოცულობა. ჩარლზის კანონი მათემატიკურად შეიძლება დაიწეროს შემდეგნაირად:
V/T=const როდესაც n, P=const.
გეი-ლუსაკის კანონი დაწერილია შემდეგნაირად:
P/T=const როდესაც n, V=const.
თუ ორივე ტოლობა წარმოდგენილია გრაფიკის სახით, მაშინ მივიღებთ სწორ ხაზებს, რომლებიც დახრილია x-ღერძის მიმართ გარკვეული კუთხით. ამ ტიპის გრაფიკი მიუთითებს პირდაპირ პროპორციულობას მოცულობასა და ტემპერატურას შორის მუდმივ წნევაზე და წნევასა და ტემპერატურას შორის მუდმივ მოცულობაზე.
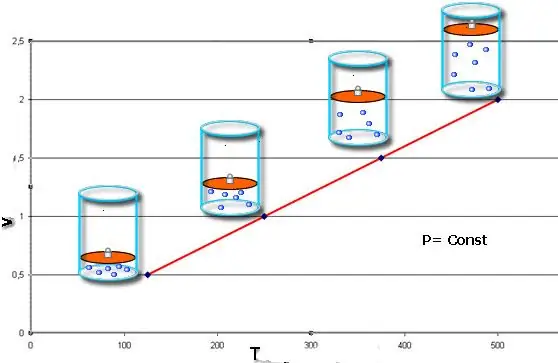
გაითვალისწინეთ, რომ სამივე განხილული გაზის კანონი არ ითვალისწინებს გაზის ქიმიურ შემადგენლობას, ისევე როგორც მისი მატერიის რაოდენობის ცვლილებას.
აბსოლუტური ტემპერატურა
ყოველდღიურ ცხოვრებაში ჩვენ მიჩვეულები ვართ ცელსიუსის ტემპერატურის სკალის გამოყენებას, რადგან ის მოსახერხებელია ჩვენს ირგვლივ მიმდინარე პროცესების აღსაწერად. ასე რომ, წყალი ადუღდება 100 oC-ზე და იყინება 0 oC-ზე. ფიზიკაში ეს სასწორი არასასიამოვნო გამოდის, ამიტომ გამოიყენება ეგრეთ წოდებული აბსოლუტური ტემპერატურის სკალა, რომელიც ლორდ კელვინმა შემოიღო XIX საუკუნის შუა ხანებში. ამ სკალის შესაბამისად, ტემპერატურა იზომება კელვინში (K).
მიჩნეულია, რომ -273, 15 oC ტემპერატურაზე არ არის ატომებისა და მოლეკულების თერმული ვიბრაციები, მათი წინ მოძრაობა მთლიანად ჩერდება. ეს ტემპერატურა ცელსიუსში შეესაბამება აბსოლუტურ ნულს კელვინში (0 K). ამ განსაზღვრებიდანაბსოლუტური ტემპერატურის ფიზიკური მნიშვნელობა შემდეგია: ეს არის მატერიის შემადგენელი ნაწილაკების კინეტიკური ენერგიის საზომი, მაგალითად, ატომები ან მოლეკულები.
გარდა აბსოლუტური ტემპერატურის ზემოთ მოცემული ფიზიკური მნიშვნელობისა, არსებობს სხვა მიდგომები ამ სიდიდის გასაგებად. ერთ-ერთი მათგანია ჩარლზის აღნიშნული გაზის კანონი. მოდით დავწეროთ შემდეგი ფორმით:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
ბოლო თანასწორობა ამბობს, რომ სისტემაში ნივთიერების გარკვეული რაოდენობით (მაგალითად, 1 მოლი) და გარკვეული წნევის დროს (მაგალითად, 1 Pa), გაზის მოცულობა ცალსახად განსაზღვრავს აბსოლუტურ ტემპერატურას. სხვა სიტყვებით რომ ვთქვათ, ამ პირობებში გაზის მოცულობის გაზრდა შესაძლებელია მხოლოდ ტემპერატურის მატების გამო, ხოლო მოცულობის შემცირება მიუთითებს T-ის მნიშვნელობის შემცირებაზე.
შეგახსენებთ, რომ ცელსიუსის ტემპერატურისგან განსხვავებით, აბსოლუტური ტემპერატურა არ შეიძლება იყოს უარყოფითი.
ავოგადროს პრინციპი და აირის ნარევები
ზემოხსენებული აირის კანონების გარდა, იდეალური გაზის მდგომარეობის განტოლება ასევე მივყავართ ამედეო ავოგადროს მიერ მე-19 საუკუნის დასაწყისში აღმოჩენილ პრინციპს, რომელიც მის გვარს ატარებს. ეს პრინციპი ადგენს, რომ ნებისმიერი გაზის მოცულობა მუდმივ წნევასა და ტემპერატურაზე განისაზღვრება სისტემაში არსებული ნივთიერების რაოდენობით. შესაბამისი ფორმულა ასე გამოიყურება:
n/V=const როდესაც P, T=const.
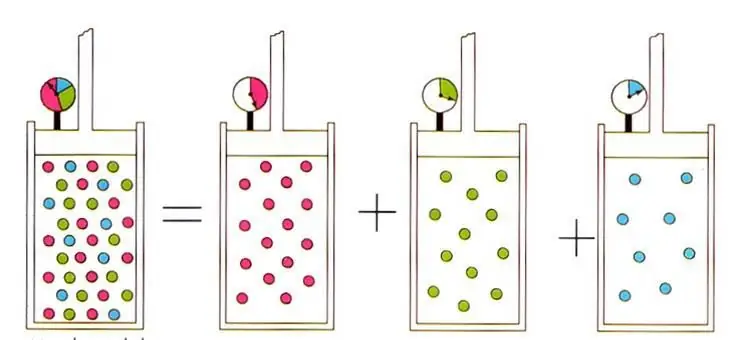
წერილობითი გამოთქმა მივყავართ იდეალურ გაზის ფიზიკაში კარგად ცნობილ დალტონის კანონს გაზის ნარევებისთვის. ესკანონი ამბობს, რომ აირის ნაწილობრივი წნევა ნარევში ცალსახად განისაზღვრება მისი ატომური წილადით.
პრობლემის გადაჭრის მაგალითი
დახურულ ჭურჭელში მყარი კედლებით, რომელიც შეიცავს იდეალურ გაზს, გახურების შედეგად წნევა 3-ჯერ გაიზარდა. აუცილებელია სისტემის საბოლოო ტემპერატურის დადგენა, თუ მისი საწყისი მნიშვნელობა იყო 25 oC.
ჯერ გადავიყვანოთ ტემპერატურა ცელსიუსის გრადუსიდან კელვინში, გვაქვს:
T=25 + 273, 15=298, 15 K.
რადგან ჭურჭლის კედლები ხისტია, გათბობის პროცესი შეიძლება ჩაითვალოს იზოქორიულად. ამ შემთხვევაში, ჩვენ ვიყენებთ გეი-ლუსაკის კანონს, გვაქვს:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
ამგვარად, საბოლოო ტემპერატურა განისაზღვრება წნევის თანაფარდობისა და საწყისი ტემპერატურის ნამრავლიდან. მონაცემების ტოლობით ჩანაცვლებით, მივიღებთ პასუხს: T2=894,45 K. ეს ტემპერატურა შეესაბამება 621,3 oC.






