ჩვენი დღევანდელი სტატიის თემა იქნება მატერიალური წერტილის კინემატიკა. რაზეა საუბარი? რა ცნებები ჩნდება მასში და რა განმარტება უნდა მიენიჭოს ამ ტერმინს? ამ და ბევრ სხვა კითხვას დღეს ვეცდებით ვუპასუხოთ.
განმარტება და კონცეფცია
მატერიალური წერტილის კინემატიკა სხვა არაფერია, თუ არა ფიზიკის ქვეგანყოფილება, რომელსაც ეწოდება "მექანიკა". ის, თავის მხრივ, სწავლობს გარკვეული სხეულების მოძრაობის ნიმუშებს. მატერიალური წერტილის კინემატიკა ასევე ეხება ამ პრობლემას, მაგრამ არ აკეთებს ამას ზოგადი გზით. სინამდვილეში, ეს ქვეგანყოფილება სწავლობს მეთოდებს, რომლებიც საშუალებას გაძლევთ აღწეროთ სხეულების მოძრაობა. ამ შემთხვევაში კვლევისთვის გამოდგება მხოლოდ ეგრეთ წოდებული იდეალიზებული სხეულები. მათ შორისაა: მატერიალური წერტილი, აბსოლუტურად ხისტი სხეული და იდეალური გაზი. მოდით განვიხილოთ ცნებები უფრო დეტალურად. სკოლის სკამიდან ყველამ ვიცით, რომ მიღებულია მატერიალურ წერტილს ვუწოდოთ სხეული, რომლის ზომები მოცემულ სიტუაციაში შეიძლება იყოს უგულებელყოფილი. სხვათა შორის, პირველად იწყება მატერიალური წერტილის მთარგმნელობითი მოძრაობის კინემატიკაჩნდება მეშვიდე კლასის ფიზიკის სახელმძღვანელოებში. ეს არის უმარტივესი ფილიალი, ამიტომ ყველაზე მოსახერხებელია მისი დახმარებით მეცნიერების გაცნობა. ცალკე საკითხია, რა არის მატერიალური წერტილის კინემატიკის ელემენტები. ისინი საკმაოდ ბევრია და პირობითად ისინი შეიძლება დაიყოს რამდენიმე დონეზე, განსხვავებული სირთულის გასაგებად. თუ ვსაუბრობთ, მაგალითად, რადიუსის ვექტორზე, მაშინ, პრინციპში, არაფერია აკრძალვით რთული მის განმარტებაში. თუმცა დამეთანხმებით, რომ მოსწავლისთვის ბევრად უფრო ადვილი იქნება მისი გაგება, ვიდრე საშუალო ან საშუალო სკოლის მოსწავლისთვის. და გულწრფელად რომ ვთქვათ, არ არის საჭირო ამ ტერმინის მახასიათებლების ახსნა საშუალო სკოლის მოსწავლეებისთვის.
კინემატიკის შექმნის მოკლე ისტორია
ბევრი, მრავალი წლის წინ, დიდმა მეცნიერმა არისტოტელემ თავისი თავისუფალი დროის ლომის წილი დაუთმო ფიზიკის, როგორც ცალკეული მეცნიერების შესწავლას და აღწერას. იგი ასევე მუშაობდა კინემატიკაზე, ცდილობდა წარმოედგინა მისი ძირითადი თეზისები და ცნებები, რომლებიც ასე თუ ისე გამოიყენებოდა პრაქტიკული და თუნდაც ყოველდღიური პრობლემების გადაჭრის მცდელობებში. არისტოტელემ წარმოადგინა საწყისი იდეები იმის შესახებ, თუ რა არის მატერიალური წერტილის კინემატიკის ელემენტები. მისი ნამუშევრები და ნამუშევრები ძალიან ღირებულია მთელი კაცობრიობისთვის. მიუხედავად ამისა, მის დასკვნებში მან დაუშვა საკმაოდ ბევრი შეცდომა და ამის მიზეზი იყო გარკვეული მცდარი წარმოდგენები და არასწორი გამოთვლები. ერთ დროს არისტოტელეს შემოქმედებით კიდევ ერთი მეცნიერი გალილეო გალილეი დაინტერესდა. არისტოტელეს მიერ წამოყენებული ერთ-ერთი ფუნდამენტური თეზისი იყო სხეულის მოძრაობახდება მხოლოდ იმ შემთხვევაში, თუ მასზე მოქმედებს რაიმე ძალა, რომელიც განისაზღვრება ინტენსივობითა და მიმართულებით. გალილეომ დაამტკიცა, რომ ეს შეცდომა იყო. ძალა გავლენას მოახდენს მოძრაობის სიჩქარის პარამეტრზე, მაგრამ არა მეტი. იტალიელმა აჩვენა, რომ ძალა არის აჩქარების მიზეზი და ის მხოლოდ ორმხრივად შეიძლება წარმოიშვას მასთან. ასევე, გალილეო გალილეიმ დიდი ყურადღება დაუთმო თავისუფალი ვარდნის პროცესის შესწავლას, შესაბამისი შაბლონების გამოყვანით. ალბათ ყველას ახსოვს მისი ცნობილი ექსპერიმენტები, რომლებიც მან პიზის დახრილ კოშკზე ჩაატარა. ფიზიკოსმა ამპერმა ასევე გამოიყენა კინემატიკური ამონახსნების საფუძვლები თავის ნაშრომებში.
საწყისი ცნებები
როგორც უკვე აღვნიშნეთ, კინემატიკა არის იდეალიზებული ობიექტების მოძრაობის აღწერის გზების შესწავლა. ამ შემთხვევაში, მათემატიკური ანალიზის საფუძვლები, ჩვეულებრივი ალგებრა და გეომეტრია შეიძლება გამოყენებულ იქნას პრაქტიკაში. მაგრამ რა ცნებები (ზუსტად ცნებები და არა პარამეტრული სიდიდეების განმარტებები) ეფუძნება ფიზიკის ამ ქვეგანყოფილებას? პირველ რიგში, ყველას ნათლად უნდა ესმოდეს, რომ მატერიალური წერტილის მთარგმნელობითი მოძრაობის კინემატიკა განიხილავს მოძრაობას ძალის მაჩვენებლების გათვალისწინების გარეშე. ანუ შესაბამისი ამოცანების გადასაჭრელად არ გვჭირდება ძალასთან დაკავშირებული ფორმულები. ამას კინემატიკა არ ითვალისწინებს, რამდენიც არ უნდა იყოს - ერთი, ორი, სამი, რამდენიმე ასეული ათასი მაინც. მიუხედავად ამისა, აჩქარების არსებობა მაინც უზრუნველყოფილია. რიგ ამოცანებში მატერიალური წერტილის მოძრაობის კინემატიკა განსაზღვრავს აჩქარების სიდიდის განსაზღვრას. თუმცა, ამ ფენომენის მიზეზები (ანუ ძალები დამათი ბუნება) არ განიხილება, მაგრამ გამოტოვებულია.
კლასიფიკაცია
ჩვენ აღმოვაჩინეთ, რომ კინემატიკა იკვლევს და იყენებს მეთოდებს სხეულების მოძრაობის აღსაწერად მათზე მოქმედი ძალების გათვალისწინების გარეშე. სხვათა შორის, ასეთ ამოცანას ეხება მექანიკის კიდევ ერთი ქვეგანყოფილება, რომელსაც დინამიკა ჰქვია. უკვე იქ გამოიყენება ნიუტონის კანონები, რომლებიც პრაქტიკაში საშუალებას იძლევა განისაზღვროს საკმაოდ ბევრი პარამეტრი მცირე რაოდენობით ცნობილი საწყისი მონაცემებით. მატერიალური წერტილის კინემატიკის ძირითადი ცნებებია სივრცე და დრო. და მეცნიერების განვითარებასთან დაკავშირებით, როგორც ზოგადად, ასევე ამ სფეროში, გაჩნდა კითხვა ასეთი კომბინაციის გამოყენების მიზანშეწონილობის შესახებ.
თავიდანვე იყო კლასიკური კინემატიკა. შეიძლება ითქვას, რომ მას ახასიათებს არა მხოლოდ როგორც დროითი, ისე სივრცითი ხარვეზების არსებობა, არამედ მათი დამოუკიდებლობა ამა თუ იმ საცნობარო ჩარჩოს არჩევისგან. სხვათა შორის, ამაზე ცოტა მოგვიანებით ვისაუბრებთ. ახლა კი ავხსნათ რაზე ვსაუბრობთ. ამ შემთხვევაში, სეგმენტი ჩაითვლება სივრცულ ინტერვალად, ხოლო დროის ინტერვალი ჩაითვლება დროებით. როგორც ჩანს, ყველაფერი ნათელია. ასე რომ, ეს ხარვეზები კლასიკურ კინემატიკაში განიხილება, როგორც აბსოლუტური, ინვარიანტული, სხვა სიტყვებით რომ ვთქვათ, დამოუკიდებლად ერთი საცნობარო ჩარჩოდან მეორეზე გადასვლისგან. იქნება თუ არა ბიზნეს რელატივისტური კინემატიკა. მასში, საცნობარო სისტემებს შორის გადასვლის დროს ხარვეზები შეიძლება შეიცვალოს. კიდევ უფრო სწორი იქნება იმის თქმა, რომ მათ არ შეუძლიათ, მაგრამ უნდა, ალბათ. ამის გამო ორივეს ერთდროულობაშემთხვევითი მოვლენები ასევე ხდება შედარებითი და ექვემდებარება განსაკუთრებულ განხილვას. სწორედ ამიტომ, რელატივისტურ კინემატიკაში ორი ცნება - სივრცე და დრო - გაერთიანებულია ერთში.
მატერიალური წერტილის კინემატიკა: სიჩქარე, აჩქარება და სხვა სიდიდეები
იმისთვის, რომ ოდნავ მაინც გაიგოთ ფიზიკის ეს ქვეგანყოფილება, თქვენ უნდა გადახედოთ ყველაზე მნიშვნელოვან ცნებებს, იცოდეთ განმარტებები და წარმოიდგინოთ, რა არის ესა თუ ის რაოდენობა ზოგადად. ამაში რთული არაფერია, სინამდვილეში ყველაფერი ძალიან მარტივი და მარტივია. განვიხილოთ, ალბათ, დასაწყისისთვის, ძირითადი ცნებები, რომლებიც გამოიყენება კინემატიკის ამოცანებში.
მოძრაობა
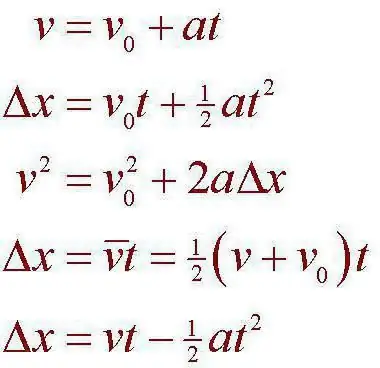
მექანიკური მოძრაობა განვიხილავთ პროცესს, რომლის დროსაც ერთი ან მეორე იდეალიზებული ობიექტი იცვლის თავის პოზიციას სივრცეში. ამ შემთხვევაში, შეგვიძლია ვთქვათ, რომ ცვლილება ხდება სხვა ორგანოებთან შედარებით. ასევე აუცილებელია გავითვალისწინოთ ის ფაქტი, რომ ორ მოვლენას შორის გარკვეული დროის ინტერვალის დადგენა ერთდროულად ხდება. მაგალითად, შესაძლებელი იქნება გარკვეული ინტერვალის იზოლირება, რომელიც წარმოიქმნება სხეულს ერთი პოზიციიდან მეორეში მოსვლას შორის. ჩვენ ასევე აღვნიშნავთ, რომ სხეულებს ამ შემთხვევაში შეუძლიათ და იქნებიან ერთმანეთთან ურთიერთქმედება, მექანიკის ზოგადი კანონების მიხედვით. სწორედ ამით მოქმედებს მატერიალური წერტილის კინემატიკა ყველაზე ხშირად. საცნობარო სისტემა არის შემდეგი კონცეფცია, რომელიც განუყოფლად არის დაკავშირებული მასთან.
კოორდინატები
მათ შეიძლება ვუწოდოთ ჩვეულებრივი მონაცემები, რომლებიც საშუალებას გაძლევთ განსაზღვროთ სხეულის პოზიცია ამა თუ იმ დროს. კოორდინატები განუყოფლად არის დაკავშირებული საცნობარო სისტემის კონცეფციასთან, ასევე კოორდინატთა ბადესთან. ყველაზე ხშირად ისინი ასოებისა და რიცხვების კომბინაციაა.
რადიუსის ვექტორი
სახელიდან უკვე გასაგები უნდა იყოს რა არის. მიუხედავად ამისა, მოდით ვისაუბროთ ამაზე უფრო დეტალურად. თუ წერტილი მოძრაობს გარკვეული ტრაექტორიის გასწვრივ და ჩვენ ზუსტად ვიცით კონკრეტული საცნობარო სისტემის დასაწყისი, მაშინ ჩვენ შეგვიძლია დავხატოთ რადიუსის ვექტორი ნებისმიერ დროს. ის დააკავშირებს წერტილის საწყის პოზიციას მყისიერ ან საბოლოო პოზიციასთან.
ტრაექტორია
მას დაერქმევა უწყვეტი ხაზი, რომელიც ჩამოყალიბებულია მატერიალური წერტილის გადაადგილების შედეგად კონკრეტულ საცნობარო სისტემაში.
სიჩქარე (როგორც წრფივი, ასევე კუთხოვანი)
ეს არის მნიშვნელობა, რომელსაც შეუძლია თქვას, რამდენად სწრაფად გადის სხეული გარკვეული მანძილის ინტერვალს.
აჩქარება (როგორც კუთხოვანი, ასევე წრფივი)
გვიჩვენებს რა კანონით და რამდენად ინტენსიურად იცვლება სხეულის სიჩქარის პარამეტრი.
ალბათ, აი, ისინი - მატერიალური წერტილის კინემატიკის ძირითადი ელემენტები. უნდა აღინიშნოს, რომ სიჩქარეც და აჩქარებაც ვექტორული სიდიდეებია. და ეს ნიშნავს, რომ მათ არა მხოლოდ აქვთ გარკვეული ინდიკატორული მნიშვნელობა, არამედ გარკვეული მიმართულებაც. სხვათა შორის, ისინი შეიძლება იყოს მიმართული როგორც ერთი მიმართულებით, ასევე საპირისპირო მიმართულებით. პირველ შემთხვევაში სხეული აჩქარდება, მეორეში კი შენელდება.
მარტივი ამოცანები
მატერიალური წერტილის კინემატიკა (სიჩქარე, აჩქარება და მანძილი, რომლებშიც პრაქტიკულად ფუნდამენტური ცნებებია) მოიცავს არა მხოლოდ ამოცანების უზარმაზარ რაოდენობას, არამედ მათ მრავალ სხვადასხვა კატეგორიას. შევეცადოთ გადავჭრათ საკმაოდ მარტივი პრობლემა სხეულის მიერ გავლილი მანძილის დადგენით.
დავუშვათ, პირობები, რომლებიც ხელთ გვაქვს, შემდეგია. მძღოლის მანქანა სასტარტო ხაზზეა. ოპერატორი დროშის შუქს აძლევს და მანქანა უეცრად აფრინდება. დაადგინეთ, შეუძლია თუ არა მას ახალი რეკორდის დამყარება მრბოლელთა შეჯიბრში, თუ მომდევნო ლიდერმა ასი მეტრი მანძილი 7,8 წამში დაფარა. აიღეთ მანქანის აჩქარება, რომელიც უდრის 3 მეტრს გაყოფილი წამის კვადრატზე.
მაშ, როგორ მოვაგვაროთ ეს პრობლემა? ეს საკმაოდ საინტერესოა, რადგან ჩვენ ვალდებულნი ვართ არ "გამშრალოთ" განსაზღვროთ გარკვეული პარამეტრები. იგი გაბრწყინებულია ბრუნვებითა და გარკვეული სიტუაციით, რაც დივერსიფიცირებს ინდიკატორების გადაჭრისა და ძიების პროცესს. მაგრამ რითი უნდა ვიხელმძღვანელოთ დავალებას მიახლოებამდე?
1. მატერიალური წერტილის კინემატიკა ითვალისწინებს ამ შემთხვევაში აჩქარების გამოყენებას.
2. ამოხსნა მიღებულია მანძილის ფორმულის გამოყენებით, რადგან მისი რიცხვითი მნიშვნელობა ჩნდება პირობებში.
პრობლემა რეალურად მოგვარებულია საკმაოდ მარტივად. ამისათვის ჩვენ ვიღებთ მანძილის ფორმულას: S=VoT + (-) AT ^ 2/2. რა აზრი აქვს? ჩვენ უნდა გავარკვიოთ, რამდენ ხანს დაფარავს მხედარი დანიშნულ მანძილს, შემდეგ კი შევადაროთ ფიგურა ჩანაწერს, რათა გავარკვიოთ, სცემს თუ არა მას. ამისათვის გამოყავით დრო, ვიღებთ ფორმულასმისთვის: AT^2 + 2VoT - 2S. ეს სხვა არაფერია, თუ არა კვადრატული განტოლება. მაგრამ მანქანა აფრინდება, რაც ნიშნავს, რომ საწყისი სიჩქარე იქნება 0. განტოლების ამოხსნისას დისკრიმინანტი ტოლი იქნება 2400-ის. დროის საპოვნელად საჭიროა ფესვის ამოღება. გავაკეთოთ მეორე ათწილადამდე: 48.98 იპოვეთ განტოლების ფესვი: 48.98/6=8.16 წამი. გამოდის, რომ მძღოლი არსებულ რეკორდს ვერ დაამარცხებს.






