ბუნებრივი გეომეტრიული ნიმუშები ან ნიმუშები ჩნდება როგორც განმეორებადი ფორმები, რომლებიც ზოგჯერ შეიძლება იყოს აღწერილი ან წარმოდგენილი მათემატიკური მოდელებით.
გეომეტრია ბუნებაში და სიცოცხლეში მოდის მრავალი ფორმით და ფორმით, როგორიცაა სიმეტრია, სპირალები ან ტალღები.
ისტორია
პირველად, ძველმა ბერძენმა ფილოსოფოსებმა და მეცნიერებმა - პითაგორამ, ემპედოკლემ და პლატონმა - განიხილეს გეომეტრიის საკითხები ბუნებაში. მცენარეებსა და ცხოველებში პროგნოზირებადი ან იდეალური გეომეტრიული ფორმების მაგალითების ანალიზით ისინი ცდილობდნენ ბუნებაში წესრიგისა და სიმეტრიის დემონსტრირებას.
ბუნებაში გეომეტრიის შესწავლის თანამედროვე მცდელობები დაიწყო მე-19 საუკუნეში ბელგიელი ფიზიკოსის ჯოზეფ პლატოს ძალისხმევით, რომელმაც შეიმუშავა საპნის ბუშტის მინიმალური ზედაპირის კონცეფცია. პირველი თანამედროვე მცდელობები თავდაპირველად კონცენტრირებული იყო იდეალური და პროგნოზირებადი გეომეტრიული ფორმების დემონსტრირებაზე, შემდეგ კი მიმართული იყო მოდელების შემუშავებაზე, რომლებიც წინასწარმეტყველებენ გეომეტრიის გამოჩენას და გამოვლინებას ბუნებაში.
მე-20 საუკუნეში მათემატიკოსი ალან ტურინგი მუშაობდა მორფოგენეზის მექანიზმებზე, რაც ხსნის ცხოველებში გარეგნობას.სხვადასხვა ნიმუშები, ზოლები, ლაქები. ცოტა მოგვიანებით, ბიოლოგი არისტიდ ლინდენმაიერი მათემატიკოს ბენუა მანდელბროტთან ერთად დაასრულებს მუშაობას მათემატიკურ ფრაქტალებზე, რომლებიც იმეორებდნენ ზოგიერთი მცენარის, მათ შორის ხეების ზრდის ნიმუშებს.
მეცნიერება
თანამედროვე მეცნიერებები (მათემატიკა, ფიზიკა და ქიმია), ტექნოლოგიებისა და მოდელების დახმარებით, ცდილობთ არა მხოლოდ ახსნათ, არამედ წინასწარ განსაზღვროთ ბუნებაში ნაპოვნი გეომეტრიული ნიმუშები.
ბევრი ცოცხალი ორგანიზმის ფორმა და ფერი, როგორიცაა ფარშევანგი, კოლიბრი და ზღვის ჭურვი, არა მხოლოდ ლამაზია, არამედ გეომეტრიულად სწორიც, რაც მეცნიერთა ცნობისმოყვარეობას იზიდავს. სილამაზე, რომელსაც ბუნებაში ვაკვირდებით, შეიძლება ბუნებრივად, მათემატიკურად იყოს გამოწვეული.
დაკვირვებული ბუნებრივი ნიმუშები მათემატიკაში აიხსნება ქაოსის თეორიით, რომელიც მუშაობს სპირალებთან და ფრაქტალებთან. ასეთი ნიმუშები ემორჩილება ფიზიკის კანონებს, გარდა ამისა, ფიზიკა და ქიმია, აბსტრაქტული მათემატიკის გამოყენებით, წინასწარმეტყველებენ კრისტალების ფორმებს, როგორც ბუნებრივ, ასევე ხელოვნურს.
ბიოლოგია ბუნებაში გეომეტრიას ხსნის ბუნებრივი გადარჩევით, სადაც ისეთი რეგულარული მახასიათებლები, როგორიცაა ზოლები, ლაქები, ნათელი ფერები, აიხსნება შენიღბვის ან სიგნალების გაგზავნის საჭიროებით.
ნიმუშების ტიპები
ბუნებაში არსებობს მრავალი განმეორებადი ნიმუში, რომლებიც ჩნდება სხვადასხვა გეომეტრიულ ფორმებში. ბუნებაში გეომეტრიის ძირითადი კანონზომიერებების ტიპები, ფოტოები და მათი აღწერილობა შეგიძლიათ იხილოთ ქვემოთ.
სიმეტრია. ეს გეომეტრიული ფორმა ბუნებაში ერთ-ერთი ყველაზე გავრცელებულია. ყველაზე გავრცელებულია ცხოველებშისარკის სიმეტრია - პეპლები, ხოჭოები, ვეფხვები, ბუები. ის ასევე გვხვდება მცენარეებში, როგორიცაა ნეკერჩხლის ფოთლები ან ორქიდეის ყვავილები. გარდა ამისა, სიმეტრიული გეომეტრია ბუნებაში შეიძლება იყოს რადიალური, ხუთსხივიანი ან ექვსჯერადი, როგორც ფიფქები.

ფრაქტალები. მათემატიკაში ეს არის საკუთარი თავის მსგავსი კონსტრუქციები, რომლებიც უსასრულოა. ბუნებაში შეუძლებელია ასეთი გაუთავებელი თვითგანმეორებადი ფორმის აღმოჩენა, ამიტომ ფრაქტალის ნიმუშების მიახლოებებს ბუნებაში გეომეტრიულ ფრაქტალებს უწოდებენ. ასეთი გეომეტრია ბუნებაში შეიმჩნევა გვიმრის ფოთლებში, ბროკოლში, ანანასის ნაყოფში.
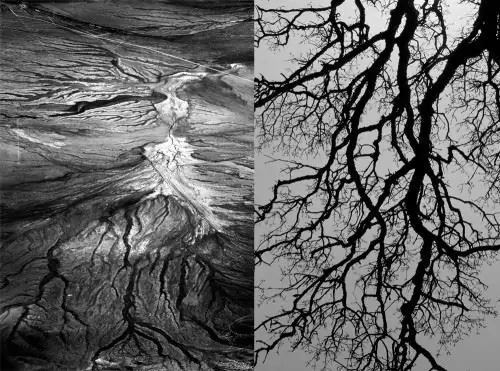
სპირალები. ეს ფორმები განსაკუთრებით გავრცელებულია მოლუსკებსა და ლოკოკინებს შორის. მეცნიერები აკვირდებიან სპირალურ ფორმებს სივრცეში, მაგალითად, სპირალურ გალაქტიკებს. სპირალს ფიბონაჩის ოქროს თანაფარდობა ეწოდება.

მეანდერსი. მათემატიკაში დინამიური სისტემების შემთხვევითობა ბუნებაში ვლინდება ისეთი ფორმებით, როგორიცაა მეანდერები და ნაკადები. ბუნებრივი გეომეტრია ღებულობს გატეხილი ან უფრო სწორად მრუდი ხაზის ფორმას, როგორიცაა მდინარის დინება.
ტალღები. ისინი გამოწვეულია ჰაერის, ქარის დინების დარღვევითა და მოძრაობებით, რომლებიც ვრცელდება როგორც ჰაერში, ასევე წყალში. ბუნებაში ეს არის არა მხოლოდ ზღვის ტალღები, არამედ უდაბნოს დიუნები, რომლებსაც შეუძლიათ გეომეტრიული ფორმების შექმნა - ხაზები, ნახევარმთვარეები და პარაბოლები.
მოზაიკა. შექმნილია ზედაპირზე იგივე ელემენტების გამეორებით. მოზაიკური გეომეტრია ველურ ბუნებაში გვხვდება ფუტკრებში: ისინი აშენებენთაფლის ჭურვი - განმეორებადი უჯრედები.

ნიმუშების ფორმირება
ბიოლოგიაში გეომეტრიული ფერის ფორმირება ბუნებრივი გადარჩევის პროცესით არის განპირობებული. ჯერ კიდევ მე-20 საუკუნის შუა ხანებში ალან ტურინგმა მოახერხა ცხოველების ფერში ლაქებისა და ზოლების გაჩენის მექანიზმის აღწერა - მან მას რეაქცია-დიფუზიის მოდელი უწოდა. სხეულის ზოგიერთი უჯრედი შეიცავს გენებს, რომლებიც კონტროლდება ქიმიური რეაქციებით. მორფოგენი იწვევს კანის მუქი პიგმენტის მქონე უბნების წარმოქმნას (ლაქები და ზოლები). თუ მორფოგენი არის კანის ყველა უჯრედში - მიიღება ვეფხისტყაოსნის ფერი, თუ ის არათანაბრად არის - ჩვეულებრივი ლაქიანი ლეოპარდი.






