პირამიდა პრიზმასთან ერთად არის სრულყოფილი პოლიედონი სამგანზომილებიან სივრცეში, მათი გეომეტრიული მახასიათებლები შესწავლილია საშუალო სკოლაში. ამ სტატიაში განვიხილავთ რა არის პირამიდები, რა ელემენტებისაგან შედგება ისინი და ასევე მოკლედ დავახასიათებთ სწორ პირამიდებს.
გეომეტრიული ფიგურის პირამიდა
გეომეტრიის თვალსაზრისით, პირამიდა არის სივრცითი ფიგურა, რომელიც შედგება ერთი მრავალკუთხედისა და რამდენიმე სამკუთხედისგან. ამ ფიგურის მიღება საკმაოდ მარტივია. ამისათვის აიღეთ მრავალკუთხედი n გვერდით, შემდეგ აირჩიეთ სივრცეში თვითნებური წერტილი, რომელიც არ იქნება მრავალკუთხედის სიბრტყეში და დააკავშირეთ მრავალკუთხედის თითოეული წვერო ამ წერტილთან. ცხადია, ამ გზით წარმოქმნილ ფიგურას ექნება n სამკუთხედი, რომლებიც დაკავშირებულია ერთმანეთთან ერთ წვეროზე.
აღწერილი ფიგურის გეომეტრიული ფორმის ვიზუალიზაციისთვის გადავიღოთ სურათი.

ეს გვიჩვენებს ოთხკუთხა პირამიდას, რომლის ფუძეაოთხკუთხედი და გვერდითი ზედაპირი შედგება ოთხი სამკუთხედისგან, რომლებსაც აქვთ საერთო წვერო.
პირამიდის ელემენტები
როგორც ნებისმიერი პოლიედონი, პირამიდაც სამი ტიპის ელემენტისგან შედგება:
- კიდეები;
- ტოპები;
- ნეკნები.
სახები არის სიბრტყეების ნაწილები, რომლებიც გამოყოფენ ფიგურის შიდა მოცულობას მიმდებარე სივრცისგან. თუ პირამიდის ფუძე შეიცავს n-გონს, მაშინ მისი სახეების რაოდენობა ყოველთვის არის n+1. აქედან n გვერდი სამკუთხაა და ერთი მხარე არის აღნიშნული n-გონალური ფუძე.
ვერტიკები არის წერტილები, სადაც ფიგურის სამი ან მეტი სახე იკვეთება. ბაზის რეგიონი შეიცავს n წვეროს, რომელთაგან თითოეული იქმნება ორი სამკუთხა სახიდან და ფუძით. წერტილს, სადაც n სამკუთხა გვერდი ხვდება, პირამიდის მწვერვალი ეწოდება. ამრიგად, განხილული ფიგურა შედგება n+1 წვეროსაგან.
კიდეები არის სწორი ხაზები, რომლებიც ჩნდება, როდესაც ორი სახე იკვეთება. თითოეული კიდე შემოსაზღვრულია ორი წვერით მის ბოლოებზე. ნებისმიერი პირამიდა n-gon ფუძით შეიცავს 2n კიდეებს. ამ რიცხვის ნახევარი, ანუ n, იქმნება მხოლოდ გვერდითი სამკუთხედების გადაკვეთით.
ფიგურების შესაძლო ტიპები
განხილული ფიგურის სახელი ცალსახად განისაზღვრება ფუძეზე მდებარე მრავალკუთხედის ტიპის მიხედვით. მაგალითად, თუ მას აქვს სამი კუთხე და სამი გვერდი, მაშინ პირამიდა იქნება სამკუთხა, თუ ოთხი - ოთხკუთხა და ასე შემდეგ.
მრავალკუთხედი შეიძლება იყოს ამოზნექილი და ჩაზნექილი, ასევე რეგულარული და ზოგადი ტიპის. ეს ყველაფერი ასევე განსაზღვრავს პირამიდის გარეგნობას.
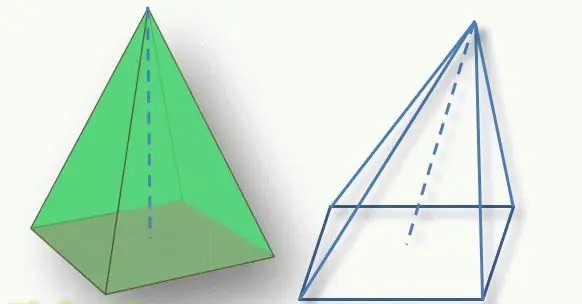
მნიშვნელოვანი პუნქტი ფიგურის ტიპის განსაზღვრისას არის პირამიდის ზედა პოზიცია მის ფუძესთან მიმართებაში. ზემოდან მრავალკუთხა ფუძემდე დახაზულ პერპენდიკულარულ სეგმენტს ფიგურის სიმაღლე ეწოდება. თუ ეს სეგმენტი კვეთს ფუძეს მის გეომეტრიულ ცენტრში (სამკუთხედისთვის ეს არის შუამავლების გადაკვეთა, ოთხკუთხედისთვის - დიაგონალების გადაკვეთა), მაშინ ფიგურას ეწოდება სწორი ხაზი. წინააღმდეგ შემთხვევაში, ისინი საუბრობენ დახრილ პირამიდაზე.
თუ ფუძის n-გონი რეგულარულია (ტოლგვერდა სამკუთხედი, კვადრატი და ა.შ.), ხოლო ფიგურა სწორია, მაშინ მას ეწოდება რეგულარული პირამიდა.
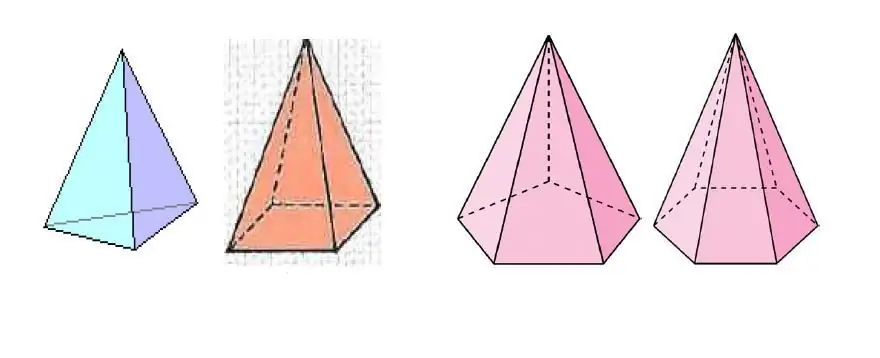
ზემოთ სურათზე ნაჩვენებია რამდენიმე პირამიდა, რომლებიც განსხვავდებიან ძირში არსებული მრავალკუთხედის გვერდების რაოდენობით.
რეგულარული პირამიდების თვისებები
ეს პირამიდები ამ კლასის სხვა ფიგურებისგან განსხვავდება სიმეტრიის მაღალი ხარისხით. ამ მხრივ მოსახერხებელია მათთან სხვადასხვა გეომეტრიული გამოთვლების ჩატარება, მაგალითად, მოცულობა ან ზედაპირის ფართობი.
რეგულარული პირამიდა შეიცავს n-გონს მის ძირში, რომლის ფართობი ცალსახად განისაზღვრება მისი მხარის სიგრძის ცოდნით. ფიგურის გვერდითი ზედაპირი იქმნება n იდენტური სამკუთხედით, რომლებიც ტოლგვერდაა. გვერდითი ზედაპირზე მდებარე ჩვეულებრივი პირამიდის კიდეები ერთმანეთის ტოლია. ამ კიდის სიგრძის მნიშვნელობა ხშირად გამოიყენება ფიგურის აპოთემის გამოთვლისა და ზედაპირის ფართობის განსაზღვრისას.
რეგულარული პირამიდის სიმაღლე ფიგურის მეორე მნიშვნელოვანი მახასიათებელია (პირველი არის კიდის სიგრძესაფუძველი). სიმაღლე გამოიყენება მოცულობის გამოთვლისას.
ბაზის პარალელურად ნებისმიერი სიბრტყე, რომელიც კვეთს პირამიდის გვერდით ნაწილებს, იწვევს მრავალკუთხა მონაკვეთის წარმოქმნას. ის ჰომოთეტურია ფუძის მრავალკუთხედის მიმართ. აღწერილი ნაჭრის ოპერაცია მივყავართ ახალი ფიგურების მთელი კლასის - დამსხვრეული რეგულარული პირამიდების ჩამოყალიბებამდე.
ყველაზე ცნობილი პირამიდები

რა თქმა უნდა, ეს არის ეგვიპტური ფარაონების რეგულარული ოთხკუთხა პირამიდები. გიზაში წოდებულ ადგილას 100-ზე მეტი ასეთი ქვის ძეგლია, რომელთა დიზაინის სრულყოფილება და გეომეტრიული პარამეტრების სიზუსტე დღემდე აოცებს მეცნიერებს. მათგან ყველაზე დიდია კეოპსის პირამიდა, რომლის სიმაღლეა დაახლოებით 146 მეტრი და სიგრძე დაახლოებით 230 მეტრი.
კონკრეტულად რას ემსახურებოდა ეს პირამიდები, ასევე რა მექანიზმებით და როდის აშენდა ისინი, დღემდე არავინ იცის.






